某射击运动员在相同条件下的射击160次，其成绩记录如下：
| 射击次数 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
| 射中9环以上的次数 |
15 |
33 |
|
63 |
79 |
97 |
111 |
130 |
| 射中9环以上的频率 |
0．75 |
0．83 |
0．80 |
0．79 |
0．79 |
|
0．79 |
0．81 |
（1）根据上表中的信息将两个空格的数据补全（射中9环以上的次数为整数，频率精确到0．01）；
（2）根据频率的稳定性，估计这名运动员射击一次时“射中9环以上”的概率（精确到0．1），并简述理由．
结合数轴与绝对值的知识回答下列问题：
（1）数轴上表示4和1的两点之间的距离是_______ ；表示-3和2两点之间的距离是_____；一般地，数轴上表示数m和数n的两点之间的距离等于|m-n|．如果表示数a和-2的两点之间的距离是3，那么a= ______
（2）若数a表示数轴上的整数点，当a取何值时,|a+1|+|a-2|的值最小，最小为多少?
（1）如图4×4的方格，每个小格的顶点叫做格点，若每个小正方形边长为1单位，请在方格中作一个正方形，同时满足下列两个条件：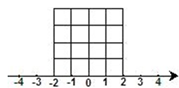
①所作的正方形的顶点，必须在方格上：
②所作正方形的面积为8个平方单位
（2）在数轴上表示实数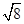
（保留作图痕迹）
一座楼梯的示意图如图所示，要在楼梯上铺一条地毯．
（1）地毯至少需多少长？（用关于a，h的代数式表示）
（2）若楼梯的宽为b，则地毯的面积为多少？
（3）当a=5m，b=1．2m，h=3m时，则地毯的面积是多少m2
把下列各数填在相应的表示集合的大括号内：
－2 ，π，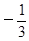
，
，
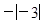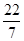，－0．3，1．7，
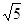，0 ， 1．1010010001…（每两个1之间依次多一个0）
整数{……}
负分数{……}
无理数{……}
观察下列等式：
第1个等式：a1=
；
第2个等式：a2=
；
第3个等式：a3=
；
第4个等式：a4=
=
×（
-
）；
…
请解答下列问题：
（1）按以上规律列出第5个等式：a5= = ；
（2）用含有n的代数式表示第n个等式：an= = （n为正整数）；
（3）求a1+a2+a3+a4+…+a100的值．