为了研究过山车的原理，物理小组提出了下列的设想：取一个与水平方向夹角为37°、长为L=2.0m的粗糙的倾斜轨道AB，通过水平轨道BC与竖直圆轨道相连，出口为水平轨道DE，整个轨道除AB段以外都是光滑的。其中AB与BC轨道以微小圆弧相接，如图所示。一个质量为2kg的小物块以初速度v0＝4.0m/s，从某一高处水平抛出，恰从A点无碰撞地沿倾斜轨道滑下。已知物块与倾斜轨道AB的动摩擦因数μ＝0.5（g取10m/s2，sin37°＝0.6，cos37°＝0.8）：
（1）求小物块的抛出点和A点的高度差；
（2）求小物块沿着轨道AB运动的过程中克服摩擦力所做的功；
（3）为了让小物块能沿着轨道运动，并从E点飞出，则竖直圆轨道的半径应该满足什么条件?
两物块A、B用轻弹簧相连，质量均为2 kg，初始时弹簧处于原长，A、B两物块都以v＝6 m／s的速度在光滑的水平地面上运动，质量4 kg的物块C静止在前方，如图所示。B与C碰撞后二者会粘在一起运动。（B和C碰撞时间极短）求在以后的运动中：
（1）当弹簧的弹性势能最大时，物块A的速度为多大?
（2）系统中弹性势能的最大值是多少?
如图所示，半径为R的半圆柱形玻璃砖某一截面的圆心为O点。有两条光线垂直于水平柱面射入玻璃砖中，其中一条光线通过圆心O，另一条光线通过A点，且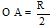
。这两条光线射出玻璃砖后相交于一点，该点到O点距离为
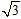R，求玻璃砖的折射率n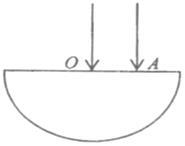
如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内，存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ，两电场的边界均是边长为L的正方形（不计电子所受重力）。
（1）在该区域AB边的中点处由静止释放电子，求电子离开ABCD区域CD边的位置.
（2）在电场Ⅰ区域内适当位置由静止释放电子，电子恰能从ABCD区域左下角D处离开，求所有释放点的位置.
（3）若将左侧电场Ⅱ整体水平向右移动L/n（n≥1），仍使电子从ABCD区域左下角D处离开（D不随电场移动），求在电场Ⅰ区域内由静止释放电子的所有位置。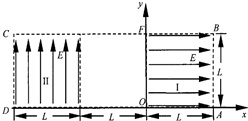
物体A的质量为mA，圆环B的质量为mB，通过绳子连接在一起，圆环套在光滑的竖直杆上，开始时连接圆环的绳子处于水平，如图所示，长度l＝4 m，现从静止释放圆环．不计定滑轮和空气的阻力，取g＝10 m/s2，求：
(1)若
，则圆环能下降的最大距离hm；
(2)若圆环下降h2＝3 m时的速度大小为4 m/s，则两个物体的质量应满足怎样的关系？
(3)若
，请定性说明小环下降过程中速度大小变化的情况及其理由。
如图所示，倾角为θ=45°的粗糙平直导轨与半径为R的光滑圆环轨道相切，切点为B，整个轨道处在竖直平面内．一质量为m的小滑块从导轨上离地面高为h=3R的D处无初速下滑并进入圆环轨道．接着小滑块从圆环最高点C水平飞出，恰好击中导轨上与圆心O等高的P点，不计空气阻力．求：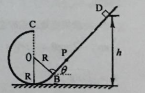
（1）滑块运动到圆环最高点C时的速度的大小；
（2）滑块运动到圆环最低点时对圆环轨道压力的大小；
（3）滑块在斜面轨道BD间运动的过程中克服摩擦力做的功。