如图（a）所示，间距为L、电阻不计的光滑导轨固定在倾角为θ的斜面上。在区域I内有方向垂直于斜面的匀强磁场，磁感应强度恒为B不变；在区域Ⅱ内有垂直于斜面向下的匀强磁场，其磁感应强度Bt的大小随时间t变化的规律如图（b）所示。t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑，同时下端的另一金属细棒cd在位于区域I内的导轨上也由静止释放。在ab棒运动到区域Ⅱ的下边界EF之前，cd棒始终静止不动，两棒均与导轨接触良好。已知cd棒的质量为0.6m、电阻为0.3R，ab棒的质量、阻值均未知，区域Ⅱ沿斜面的长度为L，在t=tx时刻（tx未知）ab棒恰好进入区域Ⅱ，重力加速度为g。求：
（1）区域I内磁场的方向；
（2）通过cd棒中的电流大小和方向；
（3）ab棒开始下滑的位置离区域Ⅱ上边界的距离；
（4）ab棒从开始下滑至EF的过程中，回路中产生总的热量。
（结果用B、L、θ、m、R、g中的字母表示）
如图所示，在光滑的水平面上有一直角坐标系，现有一个质量m=0.1kg的小球，从y轴正半轴上的P1点以速度v0=0.6m/s垂直于y轴射入。已知小球在y>0的空间内受到一个恒力F1的作用，方向沿y轴负方向，在y<0的空间内小球受到一平行于水平面、大小不变F2的作用，且F2的方向与小球的速度方向始终垂直。现小球从P1点进入坐标系后，经x=1.2m的P2点与x轴正方向成53º角射入y<0的空间，最后从y轴负半轴上的P3点垂直于y轴射出。 (已知：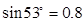
,
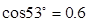)。求：
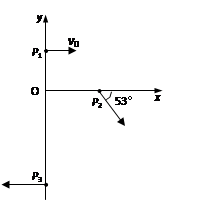
（1）P1点的坐标；
（2）F1和F2的大小。
如图所示，一个质量为m=2.0kg的滑块静止放在水平地面上的A点，受到一个大小为10N，与水平方向成θ=37°角的斜向上恒力F作用开始运动，当物体前进L=1.0m到达B点时撤去F，滑块最终停在水平地面上的C点，滑块与地面间的滑动摩擦因数µ=0.2，求BC间的距离x。（cos37o=0.8,sin37o=0.6，g取10m/s2）
长L＝0.5 m的轻杆，其一端连接着一个物体A，A的质量m＝2 kg。现让A在竖直平面内绕O点做匀速圆周运动，如图所示。在A通过最高点时，求下列两种情况下A对杆的作用力。(g＝10 m/s2)：
(1)A的速率为1 m/s；
(2)A的速率为4 m/s
如图所示，质量为3m的木板静止在光滑的水平面上，一个质量为2m的物块（可视为质点），静止在木板上的A端，已知物块与木板间的动摩擦因数为
。现有一质量为m的子弹（可视为质点）以初速度v0水平向右射入物块并穿出，已知子弹穿出物块时的速度为
，子弹穿过物块的时间极短，不计空气阻力，重力加速度为g。求：
①子弹穿出物块时物块的速度大小。
②子弹穿出物块后，为了保证物块不从木板的B端滑出，木板的长度至少多大？
如图所示，半圆形玻璃砖的半径R=10cm，折射率为n=
，直径AB与屏幕MN垂直并接触于A点。激光a以入射角i=30°射入玻璃砖的圆心O，在屏幕MN上出现了两个光斑。画出光路图并求这两个光斑之间的距离L。