如图所示，宽度为L的足够长的平行金属导轨固定在绝缘水平面上，导轨的两端连接阻值R的电阻．导轨所在空间存在竖直向下的匀强磁场，磁感应强度为B，一根质量m的导体棒MN放在导轨上与导轨接触良好，导体棒的有效电阻也为R，导体棒与导轨间的动摩擦因数为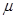
，设最大静摩擦力等于滑动摩擦力．导体棒MN的初始位置与导轨最左端距离为L，导轨的电阻可忽略不计． 
（1）若用一平行于导轨的恒定拉力F拉动导体棒沿导轨向右运动，在运动过程中保持导体棒与导轨垂直，求导体棒最终的速度；
（2）若导体棒的初速度为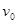
，导体棒向右运动L停止，求此过程导体棒中产生的焦耳热；
（3）若磁场随时间均匀变化，磁感应强度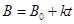
（k>0），开始导体棒静止，从t="0" 时刻起，求导体棒经过多长时间开始运动以及运动的方向．
风筝（图甲）借助于均匀的风对其作用力和牵线对其拉力的作用，才得以在空中处于平衡状态．如图乙所示，风筝平面AB与地面夹角为30°，风筝质量为300g，求风对风筝的作用力的大小．（风对风筝的作用力与风筝平面相垂直，g取10m/s2）
图中物块A重10N，A和桌面间的动摩擦因数μ=0.25，当悬挂物B重3N时，开始沿桌面滑动．求：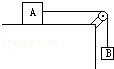
（1）B物体重1N时，A与桌面间的摩擦力多大？
（2）B物体重6N时，A与桌面的摩擦力多大？
（3）当A物体上再加上重10N的C物体，B物体重6N时，A与桌面的摩擦力多大？
一个半球形的碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的．一根细线跨在碗口上，线的两端分别系有质量为m1和 m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平线的夹角为α=60°．求两小球的质量之比
．
某汽车做匀变速直线运动，10s速度从5m/s增加到25m/s，
（1）求汽车在这段运动中的加速度大小？
（2）如果遇到紧急情况刹车，2s内速度由25m/s减到15m/s，这个过程也是匀变速直线运动，求刹车过程中的速度的大小和方向？
（3）刹车后6s末的速度为多少？
以V0=12m∕s的初速度竖直向上抛出一质量为0.5kg的物体，g取10m/s2．
求：不考虑空气阻力，小球上升的最大高度和回到抛出点的时间？