电子扩束装置由电子加速器、偏转电场和偏转磁场组成．偏转电场由加了电压的相距为d的两块水平平行放置的导体板形成，如图甲所示．大量电子（其重力不计）由静止开始，经加速电场加速后，连续不断地沿平行板的方向从两板正中间射入偏转电场．当两板不带电时，这些电子通过两板之间的时间为2t0，当在两板间加如图乙所示的周期为2t0、幅值恒为U0的电压时，所有电子均从两板间通过，然后进入水平宽度为L，竖直宽度足够大的匀强磁场中，最后通过匀强磁场打在竖直放置的荧光屏上．问：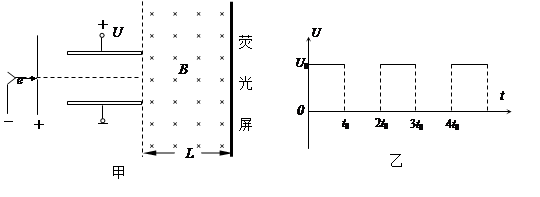
（1）电子在刚穿出两板之间时的最大侧向位移与最小侧向位移之比为多少？
（2）要使侧向位移最大的电子能垂直打在荧光屏上，匀强磁场的磁感应强度为多少？
（3）在满足第（2）问的情况下，打在荧光屏上的电子束的宽度为多少？（已知电子的质量为m、电荷量为e）
如图所示，用折射率n=
的玻璃制成的三棱镜截面。平行光线由AB面入射，从BC面射出时光线与BC面垂直。则斜射到AB面上光线的入射角是多少？斜射到AB面上的光束，并能从BC面上射出的那部分光束宽度是AB边长的多少倍？
一定质量的理想气体从状态A变化到状态B再变化到状态C，其状态变化过程的p-V图象如图所示。已知该气体在状态A时的温度为27℃。求：
①该气体在状态B、C时的温度分别为多少摄氏度？
②该气体从状态A到状态C的过程中是吸热还是放热？传递的热量是多少？
如图所示，在第一、二象限存在场强均为E的匀强电场，其中第一象限的匀强电场的方向沿x轴正方向，第二象限的电场方向沿x轴负方向。在第三、四象限矩形区域ABCD内存在垂直于纸面向外的匀强磁场，矩形区域的AB边与x轴重合。M点是第一象限中无限靠近y轴的一点，在M点有一质量为m、电荷量为e的质子，以初速度v0沿y轴负方向开始运动，恰好从N点进入磁场，若OM＝2ON，不计质子的重力，试求：
（1）N点横坐标d；
（2）若质子经过磁场最后能无限靠近M点，则矩形区域的最小面积是多少；
（3）在（2）的前提下，该质子由M点出发返回到无限靠近M点所需的时间。
（14 分）有一质量为m=2kg的小球穿在长为L=1m的轻杆顶部，轻杆与水平方向成θ=37°角。
（1）若由静止释放小球，t=1s后小球到达轻杆底端，则小球到达杆底时它所受重力的功率为多少？
（2）小球与轻杆之间的动摩擦因数为多少？
（3）若在竖直平面内给小球施加一个垂直于轻杆方向的恒力F，由静止释放小球后保持它的加速度大小a=1m/s2，且沿杆向下运动，则这样的恒力F的大小为多少？（g=l0m/s2，sin37°=0.6，cos37°=0.8）
如图所示，固定的光滑金属导轨间距为L，导轨电阻不计，上端a、b间接有阻值为R的电阻，导轨平面与水平面的夹角为θ，且处在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中。质量为m、电阻为r的导体棒与固定弹簧相连后放在导轨上。初始时刻，弹簧恰处于自然长度，导体棒具有沿轨道向上的初速度v0。整个运动过程中导体棒始终与导轨垂直并保持良好接触。已知弹簧的劲度系数为k，弹簧的中心轴线与导轨平行。
（1）求初始时刻通过电阻R的电流I的大小和方向；
（2）当导体棒第一次回到初始位置时，速度变为v，求此时导体棒的加速度大小a；
（3）导体棒最终静止时弹簧的弹性势能为Ep，求导体棒从开始运动直到停止的过程中，电阻R上产生的焦耳热Q。