(9分) 如图所示,在空间中存在垂直纸面向外、宽度为d的有界匀强磁场.一质量为m,带电荷量为q的粒子自下边界的P点处以速度v沿与下边界成30°角的方向垂直射入磁场,恰能垂直于上边界射出,不计粒子重力,题中d、m、q、v均为已知量.则:
(1)粒子带何种电荷?
(2)磁场的磁感应强度为多少?
如图,天花板下悬挂着用两根长为L=1. 0m的细线连接a、b两个小球。a球质量ma =0.7kg,b球质量为mh=0. 9kg。现在b球上施加一从零开始缓慢增大的水平力F,当F=122N时,这个力不再变化。求力F作用的服中系统增加的机械能。
如图,空间有方向垂直xoy平面的匀强磁场,磁感应强度的大小为B。坐标原点O处有一粒子源,可以在xoy平面内向各个方向发出不同速率的粒子,已知粒子电荷量为q,质量为m。A为x轴上一点,其坐标为(1,0)。(粒子重力不计)
求(1)经过A点的粒子的最小速率;
(2)若从O点发出的速率 的两个粒子都能经过A点,求这两个粒子从O点发出时速度方向间的夹角。
的两个粒子都能经过A点,求这两个粒子从O点发出时速度方向间的夹角。
两金属杆ab、cd的长度均为L,质量均为m,电阻均为R。用两根长为2L的柔软导线连接后放在光滑的水平桌面上,导线的电阻与质量不计。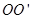 为ad、bc的中线。在
为ad、bc的中线。在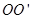 的左侧空间有垂直于桌面的匀强磁场,磁感应强度为B。位于桌子边缘的金属杆Cd受到轻微扰动就会落下桌面,当曲运动至
的左侧空间有垂直于桌面的匀强磁场,磁感应强度为B。位于桌子边缘的金属杆Cd受到轻微扰动就会落下桌面,当曲运动至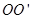 时,cd杆的加速度为零,此时Cd杆尚未着地。
时,cd杆的加速度为零,此时Cd杆尚未着地。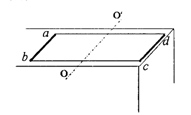
求:(1)ab杆的最大速度;
(2)ah杆从静止运动到00的过程中,回路中产生的焦耳热。
一滑雪人从静止开始沿长为200m,高为50m的雪坡匀加速滑下后,在水平面上滑行一段距离停下来。滑雪人在整个过程中受到的阻力恒为人和滑雪设备总重力的0.2倍。求滑雪人运动的总时间(结果保留整数)
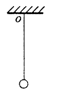
如图,长L的细绳一端固定在O点,另一端系一小球,拉动小球偏离平衡位置后释放,小球将坚直平面内作圆周运动,若细绳能承受的最大拉力为小球重力的两倍,要使小球经过最低点时细绳断裂,静止释放小球时细绳与坚直方向的夹角多大?