已知矩形的一条对角线与一边的夹角是40°,则两条对角线所成的锐角的度数是( )
| A.50° |
| B.60° |
| C.70° |
| D.80° |
如图,AB是半圆的直径,点D是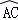 的中点,∠ABC=50°,则∠DAB等于()
的中点,∠ABC=50°,则∠DAB等于()
| A.55° | B.60° | C.65° | D.70° |
如图,AB是⊙O的直径,AB垂直于弦CD,∠BOC=70°,则∠ABD=()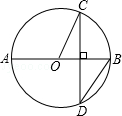
| A.20° | B.46° | C.55° | D.70° |
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()
A.2 B.8 C.2
B.8 C.2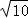 D.2
D.2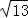
如图,▱ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为()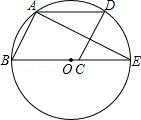
A.36° B.46° C.27° D.63°
某种手机经过四、五月份连续两次降价,每部手机由3200元降到2500元。设平均每月降价的百分率为 ,则根据题意列出的方程是().
,则根据题意列出的方程是().
A. |
B. |
C. |
D. |