已知定义在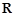 上的奇函数
上的奇函数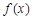 =
=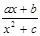 的图象如图所示,则
的图象如图所示,则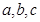 的大小关系是
的大小关系是 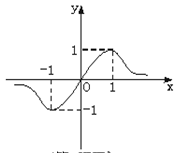
A.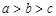 |
B. |
C.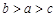 |
D.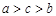 |
 参数方程
参数方程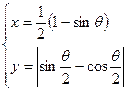
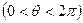 表示( )
表示( )
A.双曲线的一支,且过点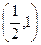 |
B.抛物线的一部分,且过点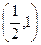 |
C.双曲线的一支,且过点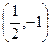 |
D.抛物 线的一部分,且过点 线的一部分,且过点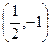 |
 设
设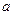 、
、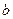 、
、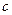 都是正实数,则
都是正实数,则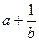 ,
,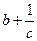 ,
,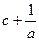 这三个数()
这三个数()
A.都不小于2 |
B.都不大于2 |
C.至少有一个 大于2 大于2 |
D.至少有一 个不小于2 个不小于2 |
 下列说法中正确的个数是()
下列说法中正确的个数是()
⑴ 回归方程只适合用我们所研究的样本的总体;
⑵ 线性回归模型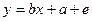 中,因变量
中,因变量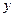 除了受自变量
除了受自变量 的影响外,可能还受到其它因素的影响,这些因素会导致随机误差e的产生;
的影响外,可能还受到其它因素的影响,这些因素会导致随机误差e的产生;
⑶ 设有一个回归方程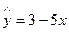 ,变量
,变量 增加一个单位时,
增加一个单位时,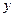 平均增加5个单位;
平均增加5个单位;
⑷ 用相关指数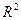 来刻画回归的效果时,
来刻画回归的效果时,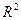 取值越大,则残差平方和越小,模型拟合的效果就越好。
取值越大,则残差平方和越小,模型拟合的效果就越好。
A.1 |
B.2 | C.3 | D.4 |
 若圆的方程为
若圆的方程为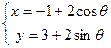 (
(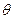 为参数),直线的方程为
为参数),直线的方程为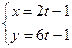 (t为参数),
(t为参数),
则直线与圆的位置关系是()。
| A.相交过圆心 | B.相交而不过圆心 | C.相切 |
D.相离 |

 设
设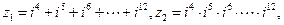 则
则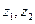 的关系是( )
的关系是( )
A.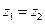 |
B. |
C.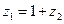 |
D.无法确定 |