先化简,再求值3a(2a2﹣4a+3)﹣2a2(3a+4),其中a=﹣2
已知2y﹣3与﹣3x﹣1成正比例,且x=2时,y=5.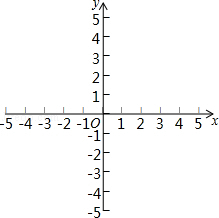
(1)求y与x之间的函数关系式,并在坐标系中画出图象;
(2)若﹣1≤y≤2,求x的取值范围;
(3)若把直线向下平移3个单位长度,那么平移后的直线的解析式为 ,请画出图象.
为了从甲、乙两名学生中选拔出一人参加今年6月份的全市中学生数学竞赛,学校每个月对他们的学习水平进行一次测验,下表是两人赛前5次的测验成绩(单位:分).
一月 二月 三月 四月 五月
甲 75 x 85 80 80
乙 65 80 80 90 95
(1)如果甲、乙两名同学5次测验成绩的平均分相等,那么甲同学二月的成绩x= ,两人的平均成绩为 ;
(2)如果你是他们的辅导教师,在它们的平均分相同的情况下你应选派哪位学生参加这次数学竞赛呢?请说明理由.
国旗法对国旗的构成由明确的规定,国旗应为长方形,长与宽的比为3:2,某学校所使用的国旗正是按这一比例制作的,长为2.4m.已知学校的旗杆高为10m,在无风的天气里,国旗会自然下垂,求国旗下垂时最低处离地面的距离是多少?(结果保留一位小数,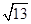 ≈3.6)
≈3.6)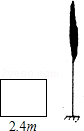
已知a= ,求
,求 的值(先化简,再求值).
的值(先化简,再求值).
已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
(1)求证:AF=DC;
(2)若AD=CF,试判断四边形AFDC是什么样的四边形?并证明你的结论.