(本小题共13分)某校有150名学生参加了中学生环保知识竞赛,为了解成绩情况,现从中随机抽取50名学生的成绩进行统计(所有学生成绩均不低于60分).请你根据尚未完成的频率分布表,解答下列问题:
| 分组 |
频数 |
频率 |
|
| 第1组 |
[60,70) |
M |
0.26 |
| 第2组 |
[70,80) |
15 |
p |
| 第3组 |
[80,90) |
20 |
0.40 |
| 第4组 |
[90,100] |
N |
q |
| 合计 |
50 |
1 |
(Ⅰ)写出M 、N 、p、q(直接写出结果即可),并作出频率分布直方图;
(Ⅱ)若成绩在90分以上的学生获得一等奖,试估计全校所有参赛学生获一等奖的人数;
(Ⅲ)现从所有一等奖的学生中随机选择2名学生接受采访,已知一等奖获得者中只有2名女生,求恰有1名女生接受采访的概率.
设函数f(x)=cos(2x+ )+sin
)+sin x.(1)求函数f(x)的最大值和最小正周期. w.w.(2)设A,B,C为
x.(1)求函数f(x)的最大值和最小正周期. w.w.(2)设A,B,C为 ABC的三个内角,若cosB=
ABC的三个内角,若cosB= ,
, ,且C为锐角,求sinA.
,且C为锐角,求sinA.
已知向量 ,向量,
,向量, 与向量
与向量 的夹角为
的夹角为 ,且
,且 ="-1" (1)求向量
="-1" (1)求向量 ; (2)设向量
; (2)设向量 =(1,0),向量
=(1,0),向量 ,其中0<
,其中0< <
<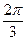 ,若
,若 =0,试求|
=0,试求| ︱的取值范围。
︱的取值范围。
已知向量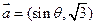 ,
,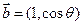 ,
,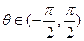 .(1)若
.(1)若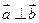 ,求
,求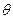 ;(2)求
;(2)求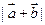 的最大值.
的最大值.
已知向量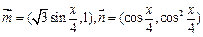 .(1)若
.(1)若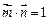 ,求
,求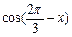 的值;(2)记
的值;(2)记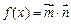 ,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围.
某班有48名同学,一次考试后数学成绩服从正态分布.平均分为80,标准差为10,问从理论上讲在80分至90分之间有多少人?