(本小题满分10分)选修4-4:极坐标于参数方程
已知曲线 (
(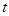 为参数),
为参数),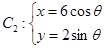 (
(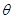 为参数).
为参数).
(1)化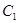 ,
, 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若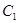 上的点
上的点 对应的参数为
对应的参数为 ,
,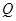 为
为 上的动点,求
上的动点,求 中点
中点 到直线
到直线 (
(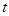 为参数)距离的最小值.
为参数)距离的最小值.
在平面直角坐标系xOy中,若双曲线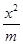 -
-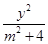 =1的离心率为
=1的离心率为 ,则m的值为________.
,则m的值为________.
已知F是椭圆C的一个焦点,B是短轴的一个端点,线段BF的延长线交C于点D,且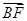 =2
=2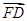 ,则C的离心率为________.
,则C的离心率为________.
若椭圆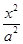 +
+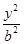 =1的焦点在x轴上,过点(1,
=1的焦点在x轴上,过点(1,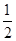 )作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________.
)作圆x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是________.
已知P为椭圆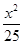 +
+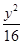 =1上的一点,M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的点,则|PM|+|PN|的最小值为________.
=1上的一点,M,N分别为圆(x+3)2+y2=1和圆(x-3)2+y2=4上的点,则|PM|+|PN|的最小值为________.
F1,F2是椭圆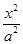 +
+ =1的左、右两焦点,P为椭圆的一个顶点,若△PF1F2是等边三角形,则a2=________.
=1的左、右两焦点,P为椭圆的一个顶点,若△PF1F2是等边三角形,则a2=________.