(本小题满分16分)已知数列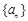 (
( ,
,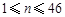 )满足
)满足 ,
, 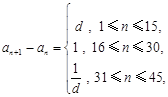 其中
其中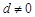 ,
, .
.
(1)当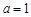 时,求
时,求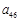 关于
关于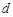 的表达式,并求
的表达式,并求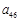 的取值范围;
的取值范围;
(2)设集合 .
.
①若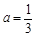 ,
,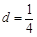 ,求证:
,求证: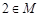 ;
;
②是否存在实数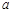 ,
,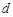 ,使
,使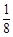 ,
,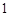 ,
,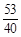 都属于
都属于 ?若存在,请求出实数
?若存在,请求出实数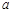 ,
,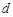 ;若不存在,请说明理由.
;若不存在,请说明理由.
如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.
(1)证明:AA1⊥BD;
(2)证明:CC1∥平面A1BD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=2,∠BAD=60°.
(1)求证:OM∥平面PAB;
(2)求证:平面PBD⊥平面PAC;
(3)当四棱锥P-ABCD的体积等于 时,求PB的长.
时,求PB的长.
如图,正方形ABCD和三角形ACE所在的平面互相垂直,EF∥BD,AB=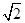 EF.
EF.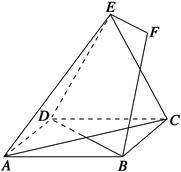
(1)求证:BF∥平面ACE;
(2)求证:BF⊥BD.
已知四棱锥PABCD的底面ABCD是边长为2的正方形,PD⊥底面ABCD,E,F分别为棱BC,AD的中点.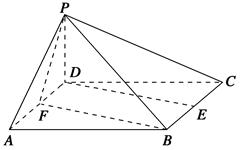
(1)求证:DE∥平面PFB;
(2)已知二面角PBFC的余弦值为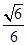 ,求四棱锥PABCD的体积.
,求四棱锥PABCD的体积.
如图,四边形ABCD是边长为2的正方形,直线l与平面ABCD平行,E和F是l上的两个不同点,且EA=ED,FB=FC.E′和F′是平面ABCD内的两点,EE′和FF′都与平面ABCD垂直.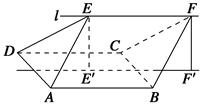
(1)证明:直线E′F′垂直且平分线段AD;
(2)若∠EAD=∠EAB=60 °,EF=2.求多面体ABCDEF的体积.