现采用随机模拟的方法估计某运动员射击4次,至少击中3次的概率：先由计算器给出0到9之间取整数值的随机数，指定0，1表示没有击中目标，2，3，4，5，6，7，8，9表示击中目标，以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数:
7527 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根据以上数据估计该射击运动员射击4次至少击中3次的概率为（ ）
A． |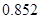
B． |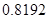
C． |
D． |
的共轭复数是a+bi（a,b
R）,i是虚数单位，则ab的值是
,若
(tÎR),则
的最小值为（）
，则
的值为（）
的图象上的所有点的横坐标缩小到原来的一半（纵坐标不变），然后把图象向左平移
个单位，则所得图形对应的函数解析式为（）
的模为
，则
= ( )
