图1和图2中，优弧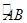所在⊙O的半径为2，AB2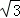．点P为优弧上一-优题课

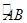图1和图2中，优弧所在⊙O的半径为2，AB=2．点P为优弧上一点（点P不与A，B重合），将图形沿BP折叠，得到点A的对称点A′．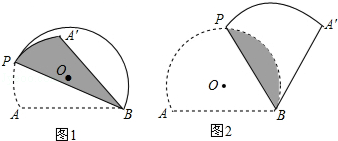

（1）点O到弦AB的距离是，当BP经过点O时，∠ABA′= °；
（2）当BA′与⊙O相切时，如图2，求折痕的长：
（3）若线段BA′与优弧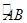只有一个公共点B，设∠ABP=α．确定α的取值范围．

科目数学题型解答题难度中等

知识点：圆幂定理

已知抛物线 $y = a x^{2} - 2 ax + 3 (a \neq 0)$ ．

（1）求抛物线的对称轴；

（2）把抛物线沿 $y$ 轴向下平移 $3 | a |$ 个单位，若抛物线的顶点落在 $x$ 轴上，求 $a$ 的值；

（3）设点 $P (a, y_{1})$ ， $Q (2, y_{2})$ 在抛物线上，若 $y_{1} > y_{2}$ ，求 $a$ 的取值范围．

如图， $AC$ 是 $⊙ O$ 的直径， $BC$ ， $BD$ 是 $⊙ O$ 的弦， $M$ 为 $BC$ 的中点， $OM$ 与 $BD$ 交于点 $F$ ，过点 $D$ 作 $DE ⊥ BC$ ，交 $BC$ 的延长线于点 $E$ ，且 $CD$ 平分 $∠ ACE$ ．

（1）求证： $DE$ 是 $⊙ O$ 的切线；

（2）求证： $∠ CDE = ∠ DBE$ ；

（3）若 $DE = 6$ ， $\tan ∠ CDE = \frac{2}{3}$ ，求 $BF$ 的长．

如图，一次函数 $y = k_{1} x + b (k_{1} \neq 0)$ 与反比例函数 $y = \frac{k_{2}}{x} (k_{2} \neq 0)$ 的图象交于点 $A (2, 3)$ ， $B (n, - 1)$ ．

（1）求反比例函数和一次函数的解析式；

（2）判断点 $P (- 2, 1)$ 是否在一次函数 $y = k_{1} x + b$ 的图象上，并说明理由；

（3）写出不等式 $k_{1} x + b ⩾ \frac{k_{2}}{x}$ 的解集．

如图，楼顶上有一个广告牌 $AB$ ，从与楼 $BC$ 相距 $15 m$ 的 $D$ 处观测广告牌顶部 $A$ 的仰角为 $37 °$ ，观测广告牌底部 $B$ 的仰角为 $30 °$ ，求广告牌 $AB$ 的高度．（结果保留小数点后一位，参考数据： $\sin 37 ° \approx 0.60$ ， $\cos 37 ° \approx 0.80$ ， $\tan 37 ° \approx 0.75$ ， $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73)$

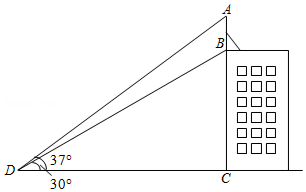
某校为了增强学生的疫情防控意识，组织全校2000名学生进行了疫情防控知识竞赛．从中随机抽取了 $n$ 名学生的竞赛成绩（满分100分），分成四组： $A : 60 ⩽ x < 70$ ； $B : 70 ⩽ x < 80$ ； $C : 80 ⩽ x < 90$ ； $D : 90 ⩽ x ⩽ 100$ ，并绘制出不完整的统计图：

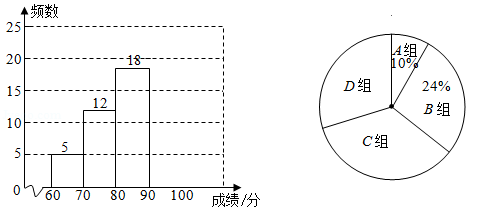
（1）填空： $n =$ 　　；

（2）补全频数分布直方图；

（3）抽取的这 $n$ 名学生成绩的中位数落在　　组；

（4）若规定学生成绩 $x ⩾ 90$ 为优秀，估算全校成绩达到优秀的人数．

试卷网试题网古诗词网作文网范文网