（本小题满分6分）如图，位于A处的海上救援中心获悉：在其北偏东68°方向的B处有一艘渔船遇险，在原地等待营救．该中心立即把消息告知在其北偏东30°且距离A点20海里的C处救生船，此时，遇险船在救生船的正东方向B处，现救生船沿着航线CB前往B处救援，求救生船到达B处行驶的距离？（参考数据：sin68°≈0.90，cos68°≈0.36，tan68°≈2.50，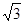
≈1.7）
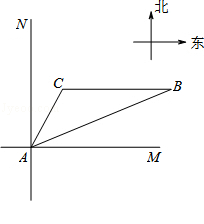
① 将下列各数填在相应的集合里。
，
，-∣
∣，
，0；
整数集合{……} 分数集合{……}
② 把表示上面各数的点画在数轴上，再按从小到大的顺序，用＂＜＂号把这些数连接起来；
若
满足
,试求代数式
的值
代入求值：
，其中
．
如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为（﹣3，0）、（0，4），抛物线y=x2+bx+c经过点B，且顶点在直线x=上．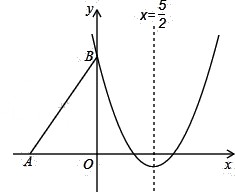
（1）求抛物线对应的函数关系式；
（2）若把△ABO沿x轴向右平移得到△DCE，点A、B、O的对应点分别是D、C、E，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；
（3）在（2）的条件下，连接BD，已知对称轴上存在一点P使得△PBD的周长最小，求出P点的坐标；
某数学研究所门前有一个边长为4米的正方形花坛，花坛内部要用红、黄、紫三种颜色的花草种植成如图所示的图案，图案中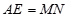
．准备在形如Rt
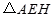的四个全等三角形内种植红色花草，在形如Rt△EMH的四个全等三角形内种植黄色花草，在正方形
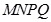内种植紫色花草，每种花草的价格如下表：
| 品种 |
红色花草 |
黄色花草 |
紫色花草 |
| 价格（元/米2） |
60 |
80 |
120 |
设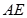
的长为
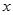米，正方形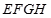
的面积为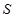
平方米，买花草所需的费用为
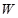元，解答下列问题：
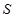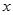（1）与之间的函数关系式为
；
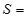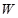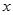（2）求与之间的函数关系式，并求所需的最低费用是多少元；
（3）当买花草所需的费用最低时，求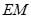
的长．