(本题共8分)某原料仓库一天的原料进出记录如下表(运进用正数表示,运出用负数表示):
| 进出数量 (单位:吨) |
-3 |
4 |
-1 |
2 |
-5 |
| 进出次数 |
2 |
1 |
3 |
3 |
2 |
(1)这天仓库的原料比原来增加了还是减少了?请说明理由;
(2)根据实际情况,现有两种方案:
方案一:运进每吨原料费用5元,运出每吨原料费用8元;
方案二:不管运进还是运出费用都是每吨原料6元;
从节约运费的角度考虑,选用哪一种方案比较合适.
(3)在(2)的条件下,设运进原料共a吨,运出原料共b吨,a、b之间满足怎样的关系时,两种方案的运费相同.
先化简,再求值:y2+(5xy-8x2)-4(xy-2x2),其中x=- ,y=2.
,y=2.
化简:2x2+1-3x+7-2x2+5x.
计算:3(x-2)-2(1+2x).
在所给的数轴上表示下列五个数,并把这五个数按从小到大的顺序,用“<”号连接起来.
-4,0,-1 ,3,2.5.
,3,2.5.
定义:P、Q分别是两条线段a和b上任意一点,线段PQ的长度的最小值叫做线段a与线段b的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.
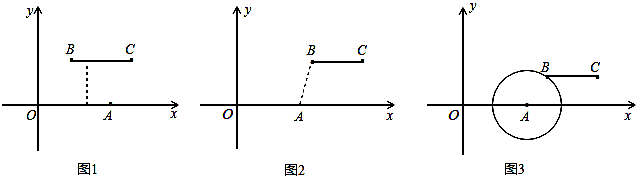
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是 ;当m=5,n=2时,如图2,线段BC与线段OA的距离为 ;
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m的值;若不存在,请说明理由.