(本小题满分12分)从广州某高校男生中随机抽取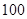 名学生,测得他们的身高(单位: cm)情况如表1:
名学生,测得他们的身高(单位: cm)情况如表1:
| 分组 |
频数 |
频率 |
 |
 |
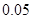 |
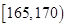 |
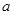 |
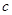 |
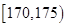 |
 |
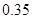 |
 |
 |
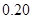 |
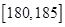 |
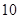 |
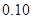 |
| 合计 |
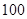 |
 |
表1
(1)求 的值;
的值;
(2)按表1的身高组别进行分层抽样, 从这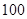 名学生中抽取
名学生中抽取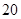 名担任广州国际马拉松志愿者, 再从身高不低于
名担任广州国际马拉松志愿者, 再从身高不低于 cm的志愿者中随机选出
cm的志愿者中随机选出 名担任迎宾工作, 求这
名担任迎宾工作, 求这 名担任迎宾工作的志愿者中至少有
名担任迎宾工作的志愿者中至少有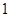 名的身高不低于
名的身高不低于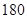 cm的概率.
cm的概率.
在直角坐标平面内,直线l过点P(1,1),且倾斜角α= .以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sinθ.
.以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=4sinθ.
(1)求圆C的直角坐标方程;
(2)设直线l与圆C交于A、B两点,求|PA|·|PB|的值.
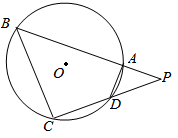
如图,四边形ABCD是圆 的内接四边形,延长BA和CD相交于点P,
的内接四边形,延长BA和CD相交于点P, ,
, .
.
(Ⅰ)求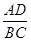 的值;
的值;
(Ⅱ)若BD为圆 的直径,且
的直径,且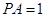 ,求BC的长.
,求BC的长.
设函数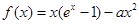 .
.
(1)若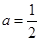 ,求的单调区间;
,求的单调区间;
(2)若当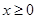 时,
时,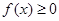 ,求
,求 的取值范围.
的取值范围.
已知定点F(3,0)和动点P(x,y),H为PF的中点,O为坐标原点,且满足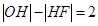 .
.
(1)求点P的轨迹方程;
(2)过点F作直线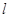 与点P的轨迹交于A,B两点,点C(2,0).连接AC,BC与直线
与点P的轨迹交于A,B两点,点C(2,0).连接AC,BC与直线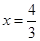 分别交于点M,N.试证明:以MN为直径的圆恒过点F.
分别交于点M,N.试证明:以MN为直径的圆恒过点F.
如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,PA=2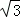 ,BC=CD=2,∠ACB=∠ACD=
,BC=CD=2,∠ACB=∠ACD= .
.
(1)求证:BD⊥平面PAC;
(2)若侧棱PC上的点F满足PF=7FC,求三棱锥P﹣BDF的体积.