已知函数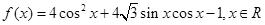
.
（1）求函数的最小正周期、最大值及取最大值时自变量的取值集合；
（2）在△ABC中，角A，B，C的对边分别是a，b，c；若a，b，c成等比数列，且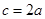
，求
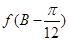的值.
函数f(x)对任意的a、b∈R,都有f(a+b)=f(a)+f(b)-1,并且当x＞0时，f(x)＞1.
（1）求证：f(x)是R上的增函数；
（2）若f(4)=5,解不等式f(3m2-m-2)＜3.
判断函数f(x)=
在定义域上的单调性.
如图所示，有一块半径为R的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O
的直径,且上底CD的端点在圆周上，写出梯形周长y关于腰长x的函数关系式，并求出它的定义域.
求函数f(x)=
的定义域.
等腰梯形ABCD的两底分别为AD=2a，BC=a，∠BAD=45°，作直线MN⊥AD交AD于M，交折线ABCD于N，记AM=x,试将梯形ABCD位于直线MN左侧的面积y表示为x的函数，并写出函数的定义域.