下图是某装置的垂直截面图,虚线A1A2是垂直截面与磁场区边界面的交线,匀强磁场分布在A1A2的右侧区域,磁感应强度B=0.4T,方向垂直纸面向外,A1A2与垂直截面上的水平线夹角为45°。A1A2的左侧,固定的薄板和等大的挡板均水平放置,它们与垂直截面交线分别为S1、S2,相距L=0.2m。在薄板上P处开一小孔,P与A1A2线上点D的水平距离为L。在小孔处装一个电子快门。起初快门开启,一旦有带正电微粒通过小孔,快门立即关闭,此后每隔T=3.0×10-3s开启一次并瞬间关闭。从S1S2之间的某一位置水平发射一速度为v0的带正电微粒,它经过磁场区域后入射到P处小孔。通过小孔的微粒与档板发生碰撞而反弹,反弹速度大小是碰前的0.5倍。(忽略微粒所受重力影响,碰撞过程无电荷转移。已知微粒的荷质比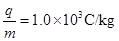 。只考虑纸面上带电微粒的运动)求:
。只考虑纸面上带电微粒的运动)求: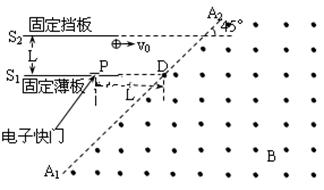
(1)满足题目的微粒在磁场中运动的半径的条件?
(2)经过一次反弹直接从小孔射出的微粒,其初速度v0应为多少?
(3)上述(2)问中微粒从最初水平射入磁场到第二次离开磁场的时间。
如图所示,质量为m,横截面为直角三角形的物块ABC,∠ABC=α,AB边靠在竖直墙面上,物块与墙面间的动摩擦因数为μ,现物块在垂直于斜面BC的推力作用下,沿墙面匀速滑动,试求出力F的大小,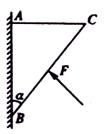
如图所示,用绳AC和BC吊起一重物,绳与竖直方向夹角分别为30°和60°,AC绳能承受的最大拉力为150N,而BC绳能承受的最大的拉力为100N,求物体最大重力不能超过多少?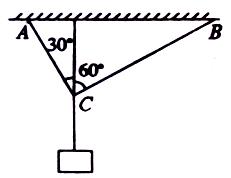
车从静止开始以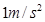 的加速度前进,在车后相距
的加速度前进,在车后相距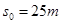 处,某人以和车运动方向相同的6m/s的速度匀速追车,问能否追上?若追不上,求人车间的最小距离为多少?
处,某人以和车运动方向相同的6m/s的速度匀速追车,问能否追上?若追不上,求人车间的最小距离为多少?
翼型飞行器有很好的飞行性能.其原理是通过对降落伞的调节,使空气升力和空气阻力都受到影响.同时通过控制动力的大小而改变飞行器的飞行状态.已知:飞行器的动力F始终与飞行方向相同,空气升力F1与飞行方向垂直,大小与速度的平方成正比,F1=C1v2;空气阻力F2与飞行方向相反,大小与速度的平方成正比,F2=C2v2.其中C1、C2相互影响,可由运动员调节,满足如图1所示的关系.飞行员和装备的总质量为90kg.(重力加速度取g=10m/s2)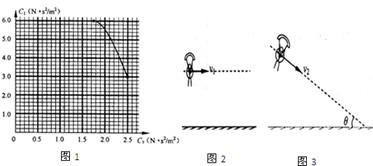
(1)若飞行员使飞行器以v 1=10 m/s速度在空中沿水平方向匀速飞行,如图2所示.则飞行器受到动力F大小为多少?
m/s速度在空中沿水平方向匀速飞行,如图2所示.则飞行器受到动力F大小为多少?
(2)若飞行员关闭飞行器的动力,使飞行器匀速滑行,且滑行速度v2与地平线的夹角θ=30°.如图3所示.则速度v2的大小为多少?(结果可用根式表示)
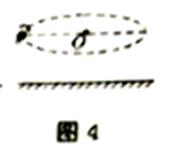
(3)若飞行员使飞行器在空中的某一水平面内做匀速圆周运动,如图4所示,在此过程中C2只能在1.75--2.5Ns2/m2之间调节,且C1、C2的大小与飞行器的倾斜程度无关,则飞行器绕行一周动力F做功的最小值为多少?(结果可保留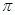 )
)
某电视娱乐节目装置可简化为如图所示模型.倾角θ=37°的斜面底端与水平传送带平滑接触,传送带BC长L=6m,始终以v0=6m/s的速度顺时针运动.将一个质量m=1kg的物块由距斜面底端高度h1=5.4m的A点静止滑下,物块通过B点时速度的大小不变.物块与斜面、物块与传送带间动摩擦因数分别为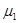 =0.5、
=0.5、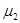 =0.2,传送带上表面距地面的高度H=5m,g取10m/s2,sin37°=0.6,cos37°=0.8
=0.2,传送带上表面距地面的高度H=5m,g取10m/s2,sin37°=0.6,cos37°=0.8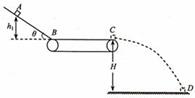
(1)求物块由A点运动到C点的时间;
(2)若把物块从距斜面底端高度h2=2.4m处静止释放,求物块落地点到C点的水平距离;
(3)求物块距斜面底端高度满足什么条件时,将物块静止释放均落到地面上的同一点D.