用反证法证明命题“三角形中必有一个内角小于或等于60°”时，首先应假设这个三角形中（ ）
| A．有一个内角大于60° |
| B．有一个内角小于60° |
| C．每一个内角都大于60° |
| D．每一个内角都小于60° |
若
是二次根式，则x的取值范围是
A． |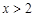
B． |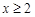
C． |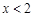
D． |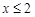
若x2+2(m－3)x+16是完全平方式，则m的值等于（）
| A．1或5 | B．5 | C．7 | D．7或－1 |
已知∠AOB=45°，点P在∠AOB内部，P1与P关于OB对称，P2与P关于OA对称，则P1、O、P2三点构成的三角形是 ( )
| A．直角三角形 | B．等腰三角形 | C．等边三角形 | D．等腰直角三角形 |
锐角三角形的三个内角是∠A、∠B、∠C，如果∠a=∠A＋∠B，∠b=∠B＋∠C，∠γ=∠C＋∠A，那么∠a、∠b、∠γ这三个角中（）．
（A）没有锐角（B）有1个锐角（C）有2个锐角（D）有3个锐角
小亮在镜中看到身后墙上的时钟如图，你认为实际时间最接近八点的是（）