如图,⊙H与x轴交于A、B两点,与y轴交于C、D两点,圆心H的坐标是(1,﹣1),半径是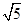 .
.
(1)求经过点D的切线的解析式;
(2)问过点A的切线与过点D的切线是否垂直?若垂直,请写出证明过程;若不垂直,请说明理由.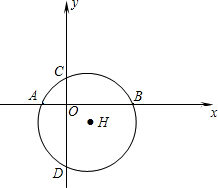
去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最少可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
下图是按一定规律排列的方程组集和它的解的集的对应关系图,若方程组集中的方程组自左至右依次记作:方程组1、方程组2、方程组3……方程组n,
(1)将方程组1的解填入图中。
(2)若方程组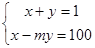 的解是
的解是 ,求m的值。
,求m的值。
(3)请依据方程组的变化规律写出方程组n(n为正整数),并解这个方程组。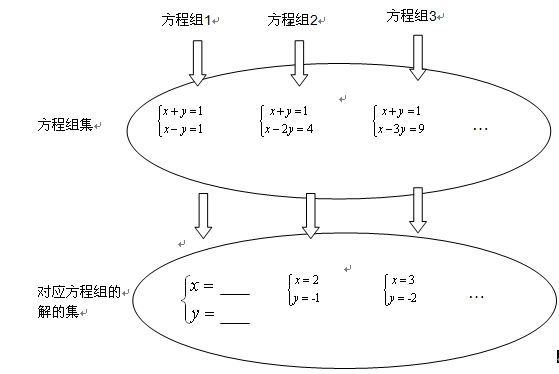
抗洪救灾小组在甲地段有28人,乙地段有15人,现在又调来29人,分配在甲乙两个地段,要求调配后甲地段人数是乙地段人数的2倍,求应调至甲地段和乙地段各多少人?
生活中,在分析研究比赛成绩时经常要考虑不等关系.例如:一射击运动员在一次比赛中将进行10次射击,已知前7次射击共中61环.如果他要打破88环(每次射击以1到10的整数环计数)的记录,问第8次射击不能少于多少环?
我们可以按以下思路分析:
首先根据最后二次射击的总成绩可能出现的情况,来确定要打破88环的记录,第8次射击需要得到的成绩,并完成下表:
| 最后二次射击总成绩 |
第8次射击需得成绩 |
| 20环 |
|
| 19环 |
|
| 18环 |
根据以上分析可得如下解答:
解:设第8次射击的成绩为x环,则可列出一个关于x的不等式:______________________________________,
解得:______________.
所以第8次射击不能少于________环.
若二元一次方程组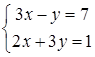 和
和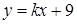 有相同解,求
有相同解,求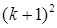 的值。
的值。