1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q ,在加速器中被加速,加速电压为U. 实际使用中,磁感应强度和加速电场频率都有最大值的限制.若某一加速器磁感应强度和加速电场频率的最大值分别为Bm、fm,加速过程中不考虑相对论效应和重力作用
A.粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比 :1 :1 |
B.粒子从静止开始加速到出口处所需的时间 |
C.如果fm> ,粒子能获得的最大动能为 ,粒子能获得的最大动能为 |
D.如果fm< ,粒子能获得的最大动能为 ,粒子能获得的最大动能为 |
一物体做匀减速直线运动,初速度大小为10 m/s,加速度大小为1 m/s2,则物体在停止运动前2 s内的平均速度大小为()
| A.0.5 m/s | B.1 m/s | C.5 m/s | D.5.5 m/s |
如图所示,A和B两物块的接触面是水平的,A与B保持相对静止一起沿固定斜面匀速下滑,在下滑过程中B的受力个数为 ( ).
| A.3个 | B.4个 | C.5个 | D.6个 |
甲、乙两汽车在平直公路上从同一地点同时开始行驶,它们的v-t图象如上图所示.忽略汽车掉头所需时间.下列对汽车运动状况的描述正确的是()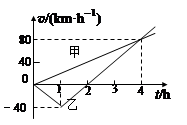
| A.在第1小时末,乙车改变运动方向 |
| B.在第4小时末,甲乙两车相遇 |
| C.在前4小时内,甲乙两车的平均速度相等 |
| D.在第2小时末,甲乙两车相距80 km |
如图所示,某人静躺在椅子上,椅子的靠背与水平面之间有固定倾斜角θ。若此人所受重力为G,则椅子对人的作用力为( )
| A.G | B.Gsinθ | C.Gcosθ | D.Gtanθ |
刀、斧、凿、刨等切削工具的刃都叫做劈,劈的截面是一个三角形,如图1-2-17所示,使用劈的时候,在劈背上加力F,这个力产生的作用效果是使劈的两侧面推压物体,把物体劈开.设劈的纵截面是一个等腰三角形,劈背的宽度是d,劈的侧面的长度是L.试求劈的两个侧面对物体的压力F1、F2.