（本大题满分12分）已知{
}是公差
≠0的等差数列，
,
,
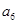成等比数列，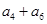
=26,数列{
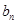}是公比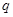
为正数的等比数列，且
=, 
=。
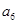（Ⅰ）求数列{},{}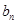的通项公式；
（Ⅱ）求数列{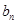}的前
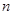项和
．
如图，AB和BC分别与圆O相切于点D、C，AC经过圆心O，且BC＝2OC.求证：AC＝2AD.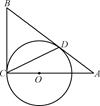
如图，在△ABC中，∠C＝90°，∠A＝60°，AB＝20，过C作△ABC的外接圆的切线CD，BD⊥CD，BD与外接圆交于点E，求DE的长．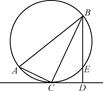
如图，AB是圆O的直径，点C在圆O上，延长BC到D使BC＝CD，过C作圆O的切线交AD于E.若AB＝6，ED＝2，求BC的值．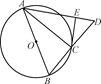
如图，PA切圆O于点A，割线PBC交圆O于点B、C，∠APC的角平分线分别与AB、AC相交于点D、E，求证：
(1)AD＝AE；
(2)AD2＝DB·EC.
如图，在△ABC中，∠B＝90°，以AB为直径的圆O交AC于D，过点D作圆O的切线交BC于E，AE交圆O于点F.求证：
(1)E是BC的中点；
(2)AD·AC＝AE·AF.