库仑定律是电学中第一个被发现的定量规律,它的发现受万有引力定律的启发。实际问题中有时需要同时考虑万有引力和库仑力,比如某无大气层的均匀带有大量负电荷的质量分布均匀的星球。将一个带电微粒置于离该星球表面一定高度处无初速释放,发现微粒恰好能静止。现给微粒一个如图所示的初速度v,则下列说法正确的是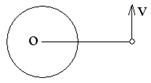
| A.微粒将做匀速直线运动 |
| B.微粒将做圆周运动 |
| C.库仑力对微粒做正功 |
| D.万有引力对微粒做正功 |
如图甲所示是一台家用台灯亮度调节原理图,理想自耦变压器AB间接入如图乙所示正弦交流电压。交流电流表A为理想表,设灯泡电阻为定值,额定电压为15V,刚开始时滑动触头P位于C位置。下列说法正确的是
| A.若要使灯泡比原来暗一些,调压端的滑动触头P应向下移动 |
| B.若将调压端的滑动触头P向下移动,电流表A的示数变大 |
| C.通过灯泡的交流电的频率为50Hz |
D.灯泡正常发光时变压器初、次级线圈的匝数比 |
如图所示,在粗糙水平面上放着一个三角形木块abc ,在它的两个粗糙斜面上分别放有质量为m1和m2的两个物体,已知m1>m2,θ1<θ2。若两物体都与三角形木块保持相对静止,以下说法正确的是
| A.水平地面对三角形木块的摩擦力水平向左 |
| B.m1受到的摩擦力与m2受到的摩擦力大小可能相等 |
| C.三角形木块对m1的作用力一定大于它对m2的作用力 |
| D.m1对三角形木块的作用力方向一定和斜面垂直 |
质量相等的两个质点A、B在拉力作用下从同一地点沿同一直线竖直向上运动的v-t图像如图所示,下列说法正确的是 
A.t2时刻两个质点在同一位置
B.0- t2时间内两质点的平均速度相等
C.0- t2时间内A质点处于超重状态
D.在t1- t2时间内质点B的机械能守恒
“月亮女神”沿距月球表面100km的轨道做匀速圆周飞行,“嫦娥一号”沿距月球表面200km的轨道做匀速圆周飞行,下列说法正确的是
| A.“月亮女神”的周期小于“嫦娥一号”的周期 |
| B.“月亮女神”的角速度小于“嫦娥一号”的角速度 |
| C.“月亮女神”的线速度小于“嫦娥一号”的线速度 |
| D.“月亮女神”的加速度小于“嫦娥一号”的加速度 |
以下叙述正确的是
| A.伽利略通过对物体运动的研究,提出了“力是维持物体运动的原因”这一观点 |
| B.牛顿在前人研究的基础上提出了牛顿第一定律,这个定律给出了惯性的概念 |
| C.楞次首先发现了电磁感应现象,使人们能够成功地将机械能转化为电能 |
| D.法拉第通过对电、磁现象的研究,首先提出了“场”的概念 |