有两段长度相等的河渠挖掘任务，分别交给甲、乙两个工程队同时进行挖掘．下图是反映所挖河渠长度y（米）与挖掘时间x（时）之间关系的部分图象．请解答下列问题：
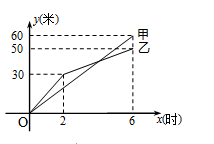
（1）乙队开挖到30米时，用了_____小时．开挖6小时时，
甲队比乙队多挖了______米；
（2）请你求出：
①甲队在0≤x≤6的时段内，y与x之间的函数关系式；
②乙队在2≤x≤6的时段内，y与x之间的函数关系式；
③开挖几小时后，甲队所挖掘河渠的长度开始超过乙队？
（3）如果甲队施工速度不变，乙队在开挖6小时后，施工速度增加到12米/时，结果两队同时完成了任务．问甲队从开挖到完工所挖河渠的长度为多少米？
解不等式或不等式组（本题10分）
（1）解不等式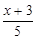
≤
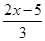-1，并在数轴上表示解集．
（2）解不等式组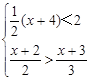
．
（本题8分）解方程组
（1）
；（2）
．
定义一种运算法则“⊕”：0⊕0=0，0⊕1=1，1⊕0=1，1⊕1=0．
（1）计算：①1⊕0⊕1⊕0=；②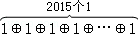
=；
（2）为提高信息在传输中的抗干扰能力，通常在原信息中按一定规则加入数据组成传输信息．
设原信息为abc，a、b、c只取0或1，传输信息为mabccn，其中m=a⊕b，n=a⊕b⊕c．如原信息010，由于0⊕1=1，0⊕1⊕0=1，所以传输信息为10101．
①若原信息是110，则传输信息为；
②下列信息：11111、01111、10101、00100、01100中，是错误的传输信息为；
③若传输信息是xyz10，则原信息为．
某市区自2014年1月起，居民生活用水开始实行阶梯式计量水价，该阶梯式计量水价分为三级（如下表所示）：
| 月用水量（吨） |
水价（元/吨） |
| 第一级 20吨以下（含20吨） |
1.6 |
| 第二级 20吨﹣30吨（含30吨） |
2.4 |
| 第三级 30吨以上 |
3.2 |
例：某用户的月用水量为32吨，按三级计量应缴交水费为：1．6×20+2．4×10+3．2×2=62．4（元）
（1）如果甲用户的月用水量为12吨，则甲需缴交的水费为元；
（2）如果乙用户缴交的水费为39．2元，则乙月用水量吨；
（3）如果丙用户的月用水量为a吨，则丙用户该月应缴交水费多少元？（用含a的代数式表示，并化简）
如图，若PE平分∠BEF，PF平分∠DFE，∠1=35°，∠2=55°，则AB与CD平行吗？为什么？