1932年,劳伦斯和利文斯设计出了回旋加速器.回旋加速器的工作原理如图所示,置于高真空中的D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计.磁感应强度为B的匀强磁场与盒面垂直.A处粒子源产生的粒子,质量为m、电荷量为+q ,在加速器中被加速,加速电压为U. 实际使用中,磁感应强度和加速电场频率都有最大值的限制.若某一加速器磁感应强度和加速电场频率的最大值分别为Bm、fm,加速过程中不考虑相对论效应和重力作用
A.粒子第2次和第1次经过两D形盒间狭缝后轨道半径之比 :1 :1 |
B.粒子从静止开始加速到出口处所需的时间 |
C.如果fm> ,粒子能获得的最大动能为 ,粒子能获得的最大动能为 |
D.如果fm< ,粒子能获得的最大动能为 ,粒子能获得的最大动能为 |
一简谐横波在图中x轴上传播,实线和虚线分别为t1和t2时刻的波形图,已知t2-t1="1.0" s,由图判断下列哪一个波速是不可能的 ( )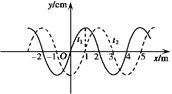
| A.1 m/s | B.3 m/s | C.5 m/s | D.10 m/s |
图甲为一列简谐横波在t=0.10s时刻的波形图,P是平衡位置为x="1" m处的质点,Q是平衡位置为x="4" m处的质点,图乙为质点Q的振动图象,则()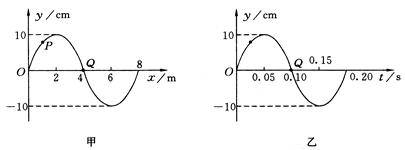
| A.t=0.15s时,质点Q的加速度达到正向最大 |
| B.t=0.15s时,质点P的运动方向沿y轴负方向 |
| C.从t=0.10s到t=0.25s,该波沿x轴正方向传播了6 m |
| D.从t=0.10s到t=0.25s,质点P通过的路程为30 cm |
一列波长大于1m的横波沿着 轴正方向传播,处在
轴正方向传播,处在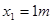 和
和 的两质点
的两质点 、
、 的振动图像如图所示。由此可知()
的振动图像如图所示。由此可知()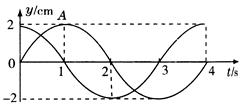
A.波长为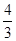 m m |
B.波速为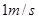 |
C.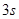 末 末 、 、 两质点的位移相同 两质点的位移相同 |
D. 末 末 点的振动速度大于 点的振动速度大于 点的振动速度 点的振动速度 |
图中实线和虚线分别是x轴上传播的一列简谐横波在t=0和t="0.03" s时刻的波形图,x="1.2" m处的质点在t="0.03" s时刻向y轴正方向运动,则()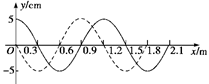
| A.该波的频率可能是125 Hz |
| B.该波的波速可能是10 m/s |
| C.t=0时x="1.4" m处质点的加速度方向沿y轴正方向 |
| D.各质点在0.03 s内随波迁移0.9 m |
做简谐振动的单摆摆长不变,若摆球质量增加为原来的4倍,摆球经过平衡位置时速度减小为原来的1/2,则单摆振动的()
| A.频率、振幅都不变 | B.频率、振幅都改变 |
| C.频率不变、振幅改变 | D.频率改变、振幅不变 |