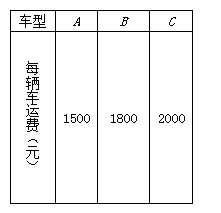
某州产苦荞茶、青花椒、野生蘑菇，为了让这些珍宝走出大山，走向世界，州政府决定组织21辆汽车装运这三种土特产共120吨，参加全国农产品博览会。现有A型、B型、C型三种汽车可供选择。已知每种型号汽车可同时装运2种土特产，且每辆车必须装满。根据下表信息，解答问题。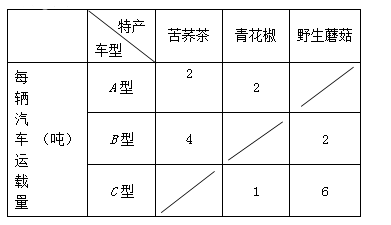
（1）设A型汽车安排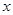
辆，B 型汽车安排
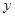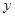辆，求与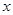之间的函数关系式。
（2）如果三种型号的汽车都不少于4辆，车辆安排有几种方案？并写出每种方案。
（3）为节约运费，应采用（2）中哪种方案？并求出最少运费。
化简：（每小题4分，共8分）
（1）
（2）
如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与x轴相交于点A（－３，０），与y轴交于点B，且与正比例函数y=
的图象交点为C（m，4）求：
（1）一次函数y=kx+b的解析式；
（2）若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，直接写出点D的坐标。
（3）在x轴上求一点P使△POC为等腰三角形，请直接写出所有符合条件的点P的坐标．
已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
（1）如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;
（2）若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.
甲、乙两车分别从相距200千米的A、B两地同时出发相向而行，甲到B地后立即返回，乙到A地后停止行驶，下图是它们离各自出发地的距离
（km）与行驶时间
（h）之间的函数图象．
（1）请直接写出甲离出发地A的距离（km）与行驶时间（h）之间的函数关系式，并写出自变量的取值范围；
（2）求出函数图像交点M的坐标并指出该点坐标的实际意义；
（3）求甲、乙两车从各自出发地驶出后经过多长时间相遇．
某医药研究所开发了一种新药，在试验时发现，如果成人按规定剂量服用2小时时血液中含药量最高，达每毫升6微克，接着逐步衰减，10小时时血液中含药量为每毫升3微克，每毫升血液中含药量y（微克）随服药后时间x（小时）的变化如图所示，当成人按规定剂量服药后。
⑴分别求出x<2与x>2时y与x的函数关系式
⑵如果每毫升血液中含药量为或3微克以上时，在治疗时是有效的，那么这个有效时间是多长？