已知直线l过点(-2,0),当直线l与圆x2+y2=2x有两个交点时,其斜率k的取值范围是( )
A.(-2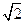 ,2 ,2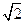 ) ) |
B.(-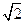 , ,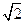 ) ) |
C.(-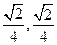 ) ) |
D.(-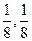 ) ) |
若原点到直线ax+by=1上的任意点距离最小值是2,则圆x2+y2=1上任一点到该直线的最大距离是( )
| A.2 | B.3 | C.1 | D.以上都有可能 |
若圆C与圆(x+2)2+(y-1)2=1关于原点对称,则圆C的方程是( )
| A.(x-2)2+(y+1)2=1 |
| B.(x-2)2+(y-1)2=1 |
| C.(x-1)2+(y+2)2=1 |
| D.(x+1)2+(y-2)2=1 |
设直线l过点(-2,0),且与圆x2+y2=1相切,则l的斜率是( )
| A.±1 | B.±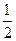 |
C.± |
D.±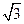 |
若直线ax+by=1与圆x2+y2=1相交,则点P(a,b)的位置是( )
| A.在圆上 | B.在圆外 |
| C.在圆内 | D.以上皆有可能 |