(本小题满分13分)已知椭圆 ,其中
,其中 为左、右焦点,且离心率
为左、右焦点,且离心率 ,直线
,直线 与椭圆交于两不同点
与椭圆交于两不同点 .当直线
.当直线 过椭圆C右焦点F2且倾斜角为
过椭圆C右焦点F2且倾斜角为 时,原点O到直线
时,原点O到直线 的距离为
的距离为 .
.
(1)求椭圆C的方程;
(2)若 ,当
,当 面积为
面积为 时,求
时,求 的最大值.
的最大值.
(本小题6分)已知直线l在两坐标轴上的截距相等,且点 到直线
到直线 的距离为
的距离为 ,求直线
,求直线 的方程.
的方程.
已知椭圆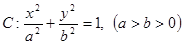 的离心率为
的离心率为 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为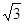 。
。
(1)求椭圆C的方程;
(2)设直线L与椭圆C交于A、B两点,坐标原点O到L的距离的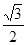 ,求△AOB面积的最大值。
,求△AOB面积的最大值。
已知正方体 中,E,F分别是
中,E,F分别是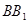 ,CD的中点
,CD的中点
(1)证明:
(2)证明:平面AED⊥
(3)设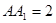 ,求三棱锥
,求三棱锥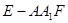 的体积。
的体积。
已知过点A(0,1)且斜率为 的直线
的直线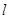 与圆C:
与圆C: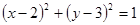 相交于M、N两点。
相交于M、N两点。
(1)求实数 的取值范围
的取值范围
(2)求证: 为定值
为定值
(3)若O为坐标原点,且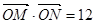 ,求K值。
,求K值。
如图,在四面体ABCD中,CB=CD,AD⊥BD,点E,F分别是AB,BD的中点。
求证:(1)直线EF∥面ACD;
(2)平面EFC⊥面BCD。