用配方法解方程x2+4x+1=0,配方后的方程是( )
| A.(x+2)2=3 | B.(x-2)2=3 | C.(x-2)2=5 | D.(x+2)2=5 |
下列运算正确的是()
| A.(a+b)(a﹣b)=a2+b2 |
| B.(a+3)2=a2+9 |
| C.a2+a2=2a4 |
| D.(﹣2a2)2=4a4 |
已知x+y=﹣5,xy=6,则x2+y2的值是()
| A.1 |
| B.13 |
| C.17 |
| D.25 |
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证()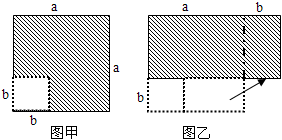
| A.(a+b)2=a2+2ab+b2 |
| B.(a﹣b)2=a2﹣2ab+b2 |
| C.a2﹣b2=(a+b)(a﹣b) |
| D.(a+2b)(a﹣b)=a2+ab﹣2b2 |
下列运算正确的是()
| A.(x﹣y)2=x2﹣y2 |
| B.x3•x2=x6 |
| C.a6÷a3=a3 |
| D.(x2)3=x5 |
如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为()
| A.(a﹣b)2=a2﹣2ab+b2 |
| B.(a+b)2=a2+2ab+b2 |
| C.a2﹣b2=(a+b)(a﹣b) |
| D.a2+ab=a(a+b) |