已知:如图①,在Rt△ACB中,∠C=90°,AC="4" cm,BC="3" cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为t(s)(0<t<2),解答下列问题: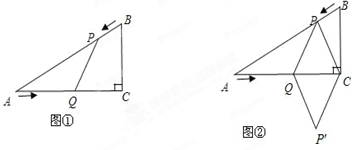
(1)当t为何值时,PQ∥BC;
(2)设△AQP的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
(4)如图②,连接PC,并把△PQC沿QC翻折,得到四边形PQP′C,那么否存在某一时刻t,使四边形PQP′C为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,求证:BC=3AD.
如图,等边△ABC中,点D、E分别是边AB、AC的中点,CD、BE交于点O,求∠BOC是多少度?
如图,△ABC中,AB=AC=10,BC=8,AD平分∠BAC交BC于点D,点E为AC的中点,连接DE,求△CDE的周长。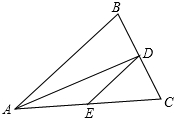
如图,在△ABC中,∠B=30°,BC的垂直平分线交AB于E,垂足为D.若ED=5,求CE的长.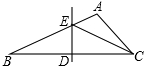
下面是小明同学在学了等腰三角形后所做的一道题,题目是这样的:“已知△ABC是等腰三角形,BC边上的高恰好等于BC边长的一半,求∠BAC的度数。”
解:如图,∵AD⊥BC,AD= BC=BD=CD,
BC=BD=CD,
∴∠BAD=∠B=∠C=∠CAD=45°,
∴∠BAC=90°
你认为小明的解答正确吗?若不正确,请你将它补充完整。