(理科)在平面直角坐标系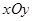 中,椭圆
中,椭圆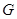 的中心为坐标原点,左焦点为
的中心为坐标原点,左焦点为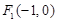 ,
, 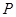 为椭圆
为椭圆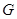 的上顶点,且
的上顶点,且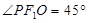 .
.
(Ⅰ)求椭圆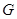 的标准方程;
的标准方程;
(Ⅱ)已知直线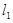 :
: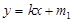 与椭圆
与椭圆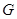 交于
交于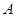 ,
,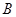 两点,直线
两点,直线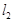 :
: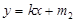 (
(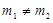 )与椭圆
)与椭圆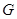 交于
交于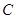 ,
,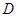 两点,且
两点,且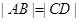 ,如图所示.
,如图所示.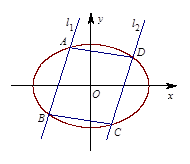
(ⅰ)证明: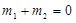 ;
;
(ⅱ)求四边形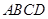 的面积
的面积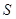 的最大值.
的最大值.
已知函数 .
.
(1)求函数f(x)的单调增区间.
(2)对任意 ,使得f(1)是函数f(x)在区间
,使得f(1)是函数f(x)在区间 上的最大值,求实数b的取值范围.
上的最大值,求实数b的取值范围.
已知椭圆E: 的离心率
的离心率 ,并且经过定点
,并且经过定点
(1)求椭圆E的方程;
(2)问是否存在直线y=-x+m,使直线与椭圆交于A,B两点,满足 ,若存在求m值,若不存在说明理由.
,若存在求m值,若不存在说明理由.
一个多面体的直观图及三视图如图所示,其中M ,N 分别是AF、BC 的中点

(1)求证:MN∥平面CDEF;
(2)求多面体A-CDEF的体积.
在某大学自主招生考试中,所有选报II类志向的考生全部参加了数学与语文两个科目的考试,成绩分为A,B,C,D,E五个等级,某考场考生的两科考试成绩的数据统计如下图,已知该考场中数学科目成绩为B的考生有10人.
(1)求该考场考生中语文科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分,求该考场考生数学科目平均分;
(3)已知本考场考生中,恰有2人的两科成绩均为A,在至少一科成绩为A的考生中,随机抽取2人进行访谈,求这2人的两科成绩均为A的概率.
已知 中,a,b,c 为角A,B,C 所对的边,
中,a,b,c 为角A,B,C 所对的边, .
.
(1)求cos A的值;
(2)若 的面积为
的面积为 ,求b ,c 的长.
,求b ,c 的长.