如图所示，ABCD是一块边长为100 m的正方形地皮，其中AST是一半径为90 m的扇形小山，其余部分都是平地.一开发商想在平地上建一个矩形停车场，使矩形的一个顶点P在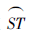
上，相邻两边CQ、CR落在正方形的边BC、CD上.求矩形停车场PQCR面积的最大值和最小值.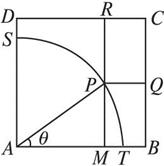
已知公差大于零的等差数列{an}的前n项和为Sn，且满足：a3·a4=117,a2+a5=22.
（1）求通项an;
(2)若数列{bn}满足bn=
,是否存在非零实数c使得{bn}为等差数列？若存在，求出c的值；若不存在，请说明理由.
设Sn是等差数列{an}的前n项和，已知
S3，
S4的等比中项为
S5; S3，S4的等差中项为1，求数列{an}的通项公式.
等差数列{an}的奇数项的和为216，偶数项的和为192，首项为1，项数为奇数，求此数列的末项和通项公式.
已知数列{an}中，a1=
，an=2-
(n≥2,n∈N*),数列{bn}满足bn=
(n∈N*).
(1)求证：数列{bn}是等差数列；
（2）求数列{an}中的最大项和最小项，并说明理由.
等差数列{an}中，a1＜0,S9=S12,该数列前多少项的和最小？