如图，在Rt△ABC中，∠C=90°，AC=BC=6，点D为AC中点，点E为边AB上一动点，点F为射线BC上一动点，且∠FDE=90°．
（1）当DF∥AB时，连接EF，求∠DEF的余切值；
（2）当点F在线段BC上时，设AE=x，BF=y，求y关于x的函数关系式，并写出x的取值范围；
（3）连接CE，若△CDE为等腰三角形，求BF的长．
如图1，对于平面上小于等于90°的∠MON，我们给出如下定义：若点P在∠MON的内部或边上，作PE⊥OM于点E，PF⊥ON于点F，则将PE+PF称为点P与∠MON的“点角距”，记作d（∠MON，P）．如图2，在平面直角坐标系xOy中，x、y正半轴所组成的角为∠xOy．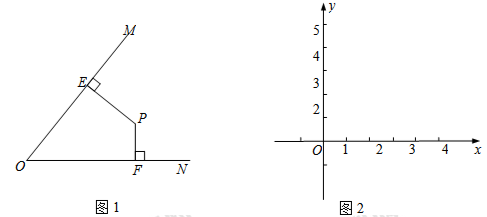
（1）已知点A（5，0）、点B（3，2），则d（∠xOy，A）= ，d（∠xOy，B）= ．
（2）若点P为∠xOy内部或边上的动点，且满足d（∠xOy，P）=5，画出点P运动所形成的图形．
（3）如图3与图4，在平面直角坐标系xOy中，射线OT的函数关系式为y=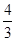
x（x≥0）．
①在图3中，点C的坐标为（4，1），试求d（∠xOT，C）的值；
②在图4中，抛物线y=-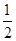
x2+2x+
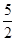经过A（5，0）与点D（3，4）两点，点Q是A，D两点之间的抛物线上的动点（点Q可与A，D两点重合），求当d（∠xOT，Q）取最大值时点Q 的坐标．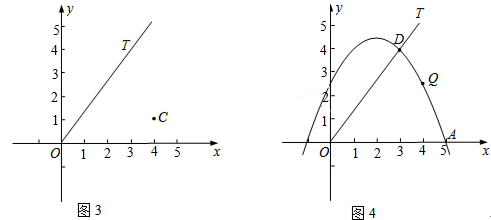
如图①，梯形ABCD中，AD∥BC，∠C=90°，BA=BC．动点E、F同时从点B出发，点E沿折线 BA-AD-DC运动到点C时停止运动，点F沿BC运动到点C时停止运动，它们运动时的速度都是1cm/s．设E出发t s时，△EBF的面积为y cm2．已知y与t的函数图象如图②所示，其中曲线OM为抛物线的一部分，MN、NP为线段．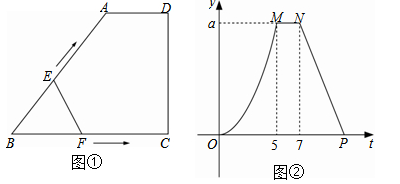
请根据图中的信息，解答下列问题：
（1）AD= cm，BC= cm；
（2）求a的值，并用文字说明点N所表示的实际意义；
（3）直接写出当自变量t为何值时，函数y的值等于5．
已知二次函数y=x2-ax-2a2（a为常数，且a≠0）．
（1）证明该二次函数的图象与x轴的正半轴、负半轴各有一个交点；
（2）若该二次函数的图象与y轴的交点坐标为（0，-2），试求该函数图象的顶点坐标．
如图，AD是⊙O的直径，AB为⊙O的弦，OP⊥AD，OP与AB的延长线交于点P．点C在OP上，且BC=PC．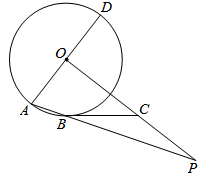
（1）求证：直线BC是⊙O的切线；
（2）若OA=3，AB=2，求BP的长．
从南京到某市可乘坐普通列车，行驶路程是520千米；也可乘坐高铁，行驶路程是400千米．已知高铁的平均速度是普通列车平均速度的2．5倍，且从南京到该市乘坐高铁比乘坐普通列车要少用3小时．求高铁行驶的平均速度．