【原创】设函数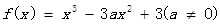
(1)若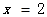 为函数
为函数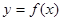 的极值点,求
的极值点,求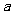 的值
的值
(2)在(1)的条件下,函数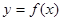 的图象的对称中心为
的图象的对称中心为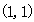 ,求
,求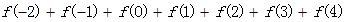 的值;
的值;
如图,在四棱锥 中,底面
中,底面 是菱形,
是菱形,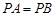 ,且侧面
,且侧面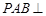 平面
平面 ,点
,点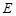 是棱
是棱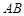 的中点.
的中点.
(Ⅰ)求证: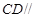 平面
平面 ;
;
(Ⅱ)求证: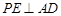 ;
;
(Ⅲ)若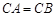 ,求证:平面
,求证:平面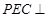 平面
平面 .
.
根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
(Ⅰ)求上图中 的值;
的值;
(Ⅱ)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(Ⅲ)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明).
函数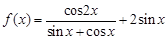 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)求函数 的最小正周期及其图象的所有对称轴的方程.
的最小正周期及其图象的所有对称轴的方程.
若函数 满足:集合
满足:集合 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数 是等比源函数.
是等比源函数.
(Ⅰ)判断下列函数:① ;②
;② ;③
;③ 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(Ⅱ)判断函数 是否为等比源函数,并证明你的结论;
是否为等比源函数,并证明你的结论;
(Ⅲ)证明: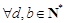 ,函数
,函数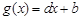 都是等比源函数.
都是等比源函数.
已知椭圆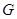 :
: 的离心率为
的离心率为 ,过椭圆
,过椭圆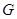 右焦点
右焦点 的直线
的直线 与椭圆
与椭圆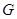 交于点
交于点 (点
(点 在第一象限).
在第一象限).
(Ⅰ)求椭圆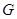 的方程;
的方程;
(Ⅱ)已知 为椭圆
为椭圆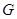 的左顶点,平行于
的左顶点,平行于 的直线
的直线 与椭圆相交于
与椭圆相交于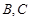 两点.判断直线
两点.判断直线 是否关于直线
是否关于直线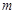 对称,并说明理由.
对称,并说明理由.