已知函数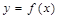 的导函数
的导函数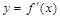 的图像如右图,则()
的图像如右图,则()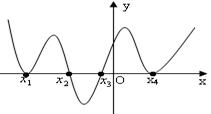
A.函数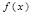 有1个极大值点,1个极小值点 有1个极大值点,1个极小值点 |
B.函数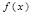 有2个极大值点,2个极小值点 有2个极大值点,2个极小值点 |
C.函数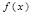 有3个极大值点,1个极小值点 有3个极大值点,1个极小值点 |
D.函数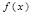 有1个极大值点,3个极小值点 有1个极大值点,3个极小值点 |
若函数 在
在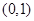 内单调递减,则实数
内单调递减,则实数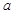 的取值范围是( )
的取值范围是( )
A. |
B.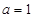 |
C.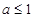 |
D.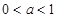 |
若 ,则
,则 =( )
=( )
| A.1 | B.0 | C.0或1 | D.以上都不对 |
函数f(x)=2x3-3x2-12x+5在[0,3]上的最大值和最小值分别是 ( )
| A.12,-15 | B.-4,-15 | C.12,-4 | D.5,-15 |
已知函数f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则实数a的取值范围是( )
| A.-1<a<2 | B.-3<a<6 | C.a<-3或a>6 | D.a<-1或a>2 |