为了了解某市课改实验区学生对新教材的喜欢程度，课改调研组从该市实验区60 000名学生中随机抽查了360名学生进行了问卷调查，并绘制出了如图所示的频数分布直方图．
（1）根据直方图中的数据制作扇形统计图（要求在图中注明各部分的百分比）．
（2）根据该调查结果，估计该市实验区约有多少名学生喜欢新教材？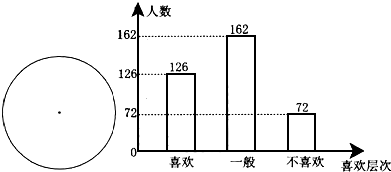
如图，为美化校园环境，某校计划在一块长为60米，宽为4米的长方形空地上修建一个长方形花圃，并将花圃四周余下的空地修建成同样宽的通道，设通道宽为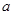
米.
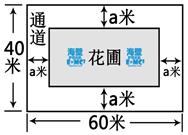
（1）用含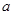的式子表示花圃的面积.
（2）如果通道所占面积是整个长方形空地面积的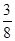
，求出此时通道的宽.
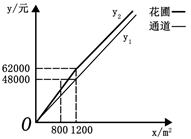
（3）已知某园林公司修建通道、花圃的造价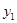
（元）、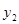
（元）与修建面积
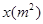之间的函数关系如图13-2所示，如果学校决定由该公司承建此项目，并要求修建的通道的宽度不少于2米且不超过10米，那么通道宽为多少时，修建的通道和花圃的总造价最低，最低总造价为多少元？
如图，在□ABCD中，E、F分别是AB、DC边上的点，且AE=CF，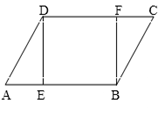
（1）求证：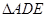
≌
.
（2）若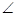
DEB=90
，求证四边形DEBF是矩形.
今年5月份，某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级（1）班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表（图11-1）和扇形统计图（图11-2）,根据图表中的信息解答下列问题:
| 分组 |
分数段 |
频数 |
| A |
36≤x＜41 |
2 2 |
| B |
41≤x＜46 |
5 |
| C |
46≤x＜51 |
15 |
| D |
51≤x＜56 |
m |
| E |
56≤x＜61 |
10 |
（1）求全班学生人数和
的值.
（2）直接学出该班学生的中考体育成绩的中位数落在哪个分数段.
（3）该班中考体育成绩满分共有3人，其中男生2人，女生1人，现需从这3人中随机选取2人到八年级进行经验交流，请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.
如图，在平面直角坐标系中，已知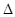
ABC的三个顶点的坐标分别为A（－1，1），B（－3,1），C（－1,4）．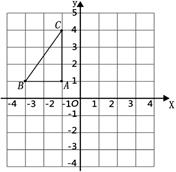
（1）画出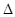ABC关于ｙ轴对称的
；
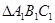（2）将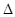ABC绕着点Ｂ顺时针旋转90
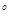后得到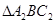
，请在图中画出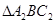，并求出线段ＢＣ旋转过程中所扫过的面积（结果保留
）．
先化简，再求值：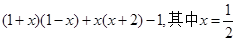
.