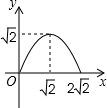
在学习掷硬币的概率时，老师说：“掷一枚质地均匀的硬币，正面朝上的概率是
”，小明做了下列三个模拟实验来验证．
①取一枚新硬币，在桌面上进行抛掷，计算正面朝上的次数与总次数的比值；
②把一个质地均匀的圆形转盘平均分成偶数份，并依次标上奇数和偶数，转动转盘，计算指针落在奇数区域的次数与总次数的比值；
③将一个圆形纸板放在水平的桌面上，纸板正中间放一个圆锥（如图），从圆锥的正上方往下撒米粒，计算其中一半纸板上的米粒数与纸板上总米粒数的比值．
上面的实验中，不科学的有（ ）
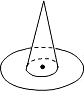
| A．0个 |
| B．1个 |
| C．2个 |
| D．3个 |
（2012辽宁营口3分）如图，菱形ABCD的边长为2，∠B=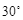
．动点P从点B出发，沿B-C-D的路线向点D运动．设△ABP的面积为
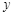(B、P两点重合时，△ABP的面积可以看做0)，点P运动的路程为
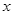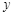，则与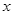之间函数关系的图像大致为（）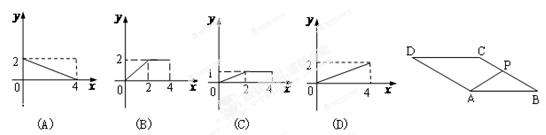
（2014年山东烟台3分）如图，点P是▱ABCD边上一动点，沿A→D→C→B的路径移动，设P点经过的路径长为x，△BAP的面积是y，则下列能大致反映y与x的函数关系的图象是（）
A． |
B． |
C． |
D． |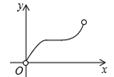
（2014年辽宁营口3分）如图，在矩形ABCD中，AB=2，AD=3，点E是BC边上靠近点B的三等分点，动点P从点A出发，沿路径A→D→C→E运动，则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是（）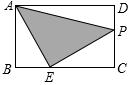
A． |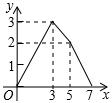
B． |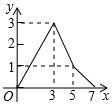
C． |
D． |
（2014年湖南岳阳3分）如图，已知点A是直线y=x与反比例函数
（k＞0，x＞0）的交点，B是图象上的另一点，BC∥x轴，交y轴于点C．动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过点P作PM⊥x轴，PN⊥y轴，垂足分别为M，N．设四边形OMPN的面积为S，P点运动时间为t，则S关于t的函数图象大致为（）
A.
B. 
C. 
D. 
（2014年福建莆田4分）如图，在矩形ABCD中，AB=2，点E在边AD上，∠ABE=45°，BE=DE，连接BD，点P在线段DE上，过点P作PQ∥BD交BE于点Q，连接QD．设PD=x，△PQD的面积为y，则能表示y与x函数关系的图象大致是（）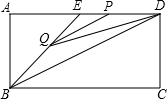
A. 
B. 
C. 
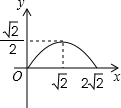D. 