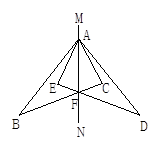如图是某公园部分景区的旅游线路示意图,其中B、C、D为风景点,A、E为路的交叉点,图中标注的数据为相应两点间的路程(单位:千米).小丽从A点出发,沿着路线A→B→E→D→A,以2千米/小时的速度游览,每个风景点的逗留时间均为0.5小时,游览回到A处时,共用3.9小时.
(1)求A→B路线(按顺时针方向)的路程;
(2)若小丽出发0.9小时后,小杰从A处出发,以3千米/小时的速度把照相机送给小丽(小杰在景点不逗留),那么小杰最快用多长时间能遇到小丽,他走的线路是怎样的?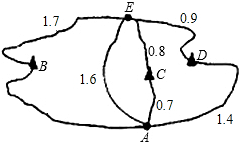
已知a-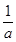 =
=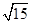 ,求a+
,求a+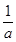 的值。
的值。
如图,点D,E在△ABC的边BC上,连 接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构成三个命题:①②⇒③:①③⇒②;②③⇒①.
(1)以上三个命题是真命题的为(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明)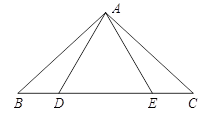
如图,在△ABC中,已知∠B=∠C
(1)尺规作图:作底角∠ABC的平分线BD,交AC于点D(作图不写作法,但保留作图痕迹);
(2)猜想:“若∠A=36°,则△ABD和△BDC都是等腰三角形”。请你通过计算说明猜想是否成立.
某质检部门抽取甲、乙两厂相同数量的产品进行质量检测,测得甲厂有合格品48件,乙厂有合格品45件,且甲厂的产品合格率比乙厂的产品合格率高5%,问甲厂产品的合格率是多少?
如图,△ABC与△ADE关于直线MN对称.BC与DE的交点F在直线MN上.
①指出两个三角形中的对称点;
②指出图中相等的线段和角;
③图中还有对称的三角形吗?