某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表
| 商店名称 |
A |
B |
C |
D |
E E |
| 销售额x(千万元) |
3 |
5 |
6 |
7 |
9 9 |
| 利润额y(千万元) |
2 |
3 |
3 |
4 |
5 |
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性。
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.
(3)当销售额为4(千万元)时,估计利润额的大小.
一个包装箱内有6件产品,其中4件正品,2件次品。现随机抽出两件产品,
(1)求恰好有一件次品的概率。
(2)求都是正品的概率。
(3)求抽到次品的概率
已知一个5次多项式为f(x)=4x5﹣3x3+2x2+5x+1,用秦九韶算法求这个多项式当x=2时的值
(每小题6分,共12分)(1)函数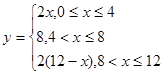 ,编写出求函数的函数值的程序(使用嵌套式);
,编写出求函数的函数值的程序(使用嵌套式);
(2)“求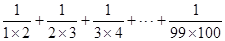 的值.”写出用基本语句编写的程序(使用当型).
的值.”写出用基本语句编写的程序(使用当型).
(本小题满分14分)已知函数 ..
..
(Ⅰ)若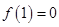 ,求函数
,求函数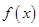 的最大值;
的最大值;
(Ⅱ)令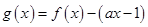 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅲ)若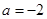 ,正实数
,正实数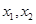 满足
满足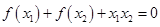 ,证明
,证明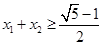 .
.