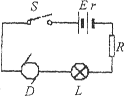如图所示,水平地面和半圆轨道面均光滑,质量M=1kg的小车静止在地面上,小车上表面与R=0.24m的半圆轨道最低点P的切线相平。现有一质量m=2kg的滑块(可视为质点)以v0=6m/s的初速度滑上小车左端,二者共速时小车还未与墙壁碰撞,当小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数μ=0.2,g取10m/s2,求: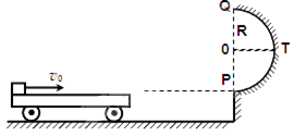
(1)滑块与小车共速时的速度及小车的最小长度;
(2)滑块m恰好从Q点离开圆弧轨道时小车的长度;
(3)讨论小车的长度L在什么范围,滑块能滑上P点且在圆轨道运动时不脱离圆轨道?
汽车A正以30m/s的速度在平直公路上行驶,司机突然发现前方一汽车B正以6m/s的速度行驶,汽车A司机立即以6m/s2的加速度刹车,若要两车不相撞,则A开始刹车时两车的距离至少应为多大?
如右图所示,一个物体在OA、OB绳两根细绳的拉力作用下保持静止,OA绳与水平天花
板间的夹角为30°,OB绳保持水平。且OA和OB绳上能承受的最大拉力均为100N,为了保证绳的安全,所挂物体的重力不得超过多少牛顿?
光滑的平行导轨倾角为θ=60度,在相距为1m的平行导轨上放一质量为0.3kg的金属棒,通过金属棒的电流是3A,磁场方向为竖直向下,这时金属棒恰好静止。
(1)匀强磁场磁感应强度的大小
(2)金属棒对导轨的压力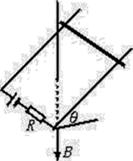
两个半径均为R的圆形平板电极,平行正对放置,相距为d,极板间的电势差为U,板间电场可以认为是均匀的。一个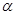 粒子(42He)从正极板边缘以某一初速度垂直于电场方向射入两极板之间,到达负极板时恰好落在极板中心。已知质子电荷为e,质子和中子的质量均视为m,忽略重力和空气阻力的影响,求:
粒子(42He)从正极板边缘以某一初速度垂直于电场方向射入两极板之间,到达负极板时恰好落在极板中心。已知质子电荷为e,质子和中子的质量均视为m,忽略重力和空气阻力的影响,求:
(1)极板间的电场强度E;
(2)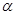 粒子在极板间运动的加速度a;
粒子在极板间运动的加速度a;
(3)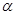 粒子的初速度v0。
粒子的初速度v0。
如图所示,已知电源电动势E=20V,内阻r=lΩ,当接入固定电阻R=4Ω时,电路中标有“3V, 6W”的灯泡L和内阻RD=0.5Ω的小型直流电动机D都恰能正常工作.试求:(1)电路中的电流大小;(2)电动机的额定电压; (3)电动机的输出功率.