如图甲所示,固定在水平桌边上的“ ”型平行金属导轨足够长,倾角为53º,间距L=2m,电阻不计;导轨上两根金属棒ab、cd的阻值分别为R1=2Ω,R2=4Ω,cd棒质量m1=1.0kg,ab与导轨间摩擦不计,cd与导轨间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力,整个导轨置于磁感应强度B=5T、方向垂直倾斜导轨平面向上的匀强磁场中。现让ab棒从导轨上某处由静止释放,当它刚要滑出导轨时,cd棒刚要开始滑动;g取10m/s2,sin37 º ="cos53" º =0.6,cos37 º =" sin53" º =0.8。
”型平行金属导轨足够长,倾角为53º,间距L=2m,电阻不计;导轨上两根金属棒ab、cd的阻值分别为R1=2Ω,R2=4Ω,cd棒质量m1=1.0kg,ab与导轨间摩擦不计,cd与导轨间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力,整个导轨置于磁感应强度B=5T、方向垂直倾斜导轨平面向上的匀强磁场中。现让ab棒从导轨上某处由静止释放,当它刚要滑出导轨时,cd棒刚要开始滑动;g取10m/s2,sin37 º ="cos53" º =0.6,cos37 º =" sin53" º =0.8。
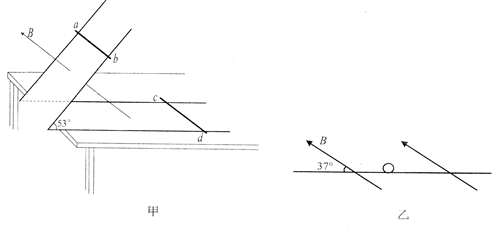
(1)在乙图中画出此时cd棒的受力示意图,并求出ab棒的速度;
(2)若ab棒无论从多高的位置释放,cd棒都不动,则ab棒质量应小于多少?
(3)假如cd棒与导轨间的动摩擦因数可以改变,则当动摩擦因数满足什么条件时,无论ab棒质量多大、从多高位置释放,cd棒始终不动?
在某中学举办的智力竞赛中,有一个叫做“保护鸡蛋”的竞赛项目。要求制作一个装置,让鸡蛋从两层楼的高度落到地面且不被摔坏。如果没有保护,鸡蛋最多只能从0.1 m的高度落到地面而不被摔坏。有一位同学设计了如图所示的一个装置来保护鸡蛋,用A、B两块较粗糙的夹板夹住鸡蛋,A夹板和B夹板与鸡蛋之间的摩擦力均为鸡蛋重力的5倍。现将该装置从距地面4 m的高处落下,装置着地时间短且保持竖直不被弹起。g取10 m/s2,不考虑空气阻力,求: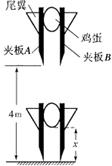
(1)如果没有保护,鸡蛋直接撞击地面而不被摔坏,其速度最大不能超过多少?
(2)如果使用该装置,鸡蛋夹放的位置离装置下端距离x至少为多少?
如图甲是一种家用电熨斗的电路原理图(额定电压为220 V).R0是定值电阻,R是可变电阻(调温开关),其电阻值均不受温度影响.
(1)该电熨斗温度最低时的耗电功率为121 W,温度最高时的耗电功率为484 W,求R0的阻值及R的阻值变化范围.
(2)假定电熨斗每秒钟散发的热量q跟电熨斗表面温度与环境温度的温差关系如图乙所示,现在温度为20 ℃的房间使用该电熨斗来熨烫毛料西服,要求熨斗表面温度为220 ℃,且保持不变,问应将R的阻值调为多大?
有一种测量压力的电子秤,其原理图如图所示。E是内阻不计、电动势为6V的电源。R0是一个阻值为400Ω的限流电阻。G是由理想电流表改装成的指针式测力显示器。R是一个压敏电阻,其阻值可随压力大小变化而改变,其关系如下表所示。C是一个用来保护显示器的电容器。秤台的重力忽略不计。试分析:
| 压力F/N |
0 |
50 |
100 |
150 |
200 |
250 |
300 |
| 电阻R/Ω |
300 |
280 |
260 |
240 |
220 |
200 |
180 |
(1)利用表中的数据归纳出电阻R随压力F变化的函数式
(2)若电容器的耐压值为5V,该电子秤的最大称量值为多少牛顿?
(3)通过寻求压力与电流表中电流的关系,说明该测力显示器的刻度是否均匀?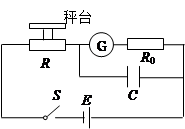

在某一旅游景区,建有一山坡滑草运动项目.该山坡可看成倾角θ=30°的斜面,一名游客连同滑草装置总质量m=80 kg,他从静止开始匀加速下滑,在时间t=5 s内沿斜面滑下的位移x=50 m.(不计空气阻力,取g=10 m/s2).问:
(1)游客连同滑草装置在下滑过程中受到的摩擦力Ff为多大?
(2)滑草装置与草皮之间的动摩擦因数μ为多大?
(3)设游客滑下50 m后进入水平草坪,试求游客在水平面上滑动的最大距离.
如图所示,处于同一条竖直线上的两个点电荷A、B带等量同种电荷,电荷量为Q;G、H 是它们连线的垂直平分线。另有一个带电小球C,质量为m、电荷量为+q(可视为点电荷),被长为l的绝缘轻细线悬挂于O点,现在把小球C拉起到M点,使细线水平且与A、B处于同一竖直面内,由静止开始释放,小球C向下运动到GH线上的N点时刚好速度为零,此时细线与竖直方向上的夹角θ=30º。试求:
⑴在A、B所形成的电场中,MN两点间的电势差,并指出M、N哪一点的电势高。
⑵若N点与A、B两个点电荷所在位置正好形成一个边长为x的正三角形,则小球运动到N点瞬间,轻细线对小球的拉力FT(静电力常量为k)。