如图①,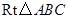 中,
中, ,
, .它的顶点
.它的顶点 的坐标为
的坐标为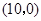 ,顶点
,顶点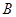 的坐标为
的坐标为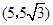 ,
,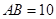 ,点
,点 从点
从点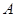 出发,沿
出发,沿 的方向匀速运动,同时点
的方向匀速运动,同时点 从点
从点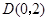 出发,沿
出发,沿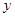 轴正方向以相同速度运动,当点
轴正方向以相同速度运动,当点 到达点
到达点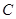 时,两点同时停止运动,设运动的时间为
时,两点同时停止运动,设运动的时间为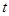 秒.
秒.
(1)求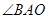 的度数.
的度数.
(2)当点 在
在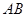 上运动时,
上运动时,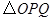 的面积
的面积 (平方单位)与时间
(平方单位)与时间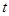 (秒)之间的函数图象为抛物线的一部分,(如图②),求点
(秒)之间的函数图象为抛物线的一部分,(如图②),求点 的运动速度.
的运动速度.
(3)求(2)中面积 与时间
与时间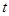 之间的函数关系式及面积
之间的函数关系式及面积 取最大值时点
取最大值时点 的坐标.
的坐标.
(4)如果点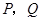 保持(2)中的速度不变,那么点
保持(2)中的速度不变,那么点 沿
沿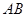 边运动时,
边运动时, 的大小随着时间
的大小随着时间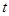 的增大而增大;沿着
的增大而增大;沿着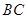 边运动时,
边运动时, 的大小随着时间
的大小随着时间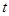 的增大而减小,当点
的增大而减小,当点 沿这两边运动时,使
沿这两边运动时,使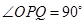 的点
的点 有几个?请说明理由.
有几个?请说明理由.
某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
| 甲 |
乙 |
|
| 进价(元/部) |
4000 |
2500 |
| 售价(元/部) |
4300 |
3000 |
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
已知抛物线 与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).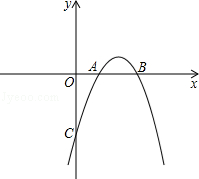
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.
2013年5月7日浙江省11个城市的空气质量指数(AQI)如图所示: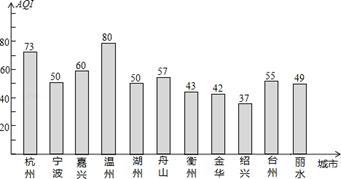
(1)这11个城市当天的空气质量指数的极差、众数和中位数分别是多少?
(2)当0≤AQI≤50时,空气质量为优.求这11个城市当天的空气质量为优的频率;
(3)求宁波、嘉兴、舟山、绍兴、台州五个城市当天的空气质量指数的平均数.
天封塔历史悠久,是宁波著名的文化古迹.如图,从位于天封塔的观测点C测得两
建筑物底部A,B的俯角分别为45°和60°,若此观测点离地面的高度为51米,A,B两点在CD的两侧,且点A,
D,B在同一水平直线上,求A,B之间的距离(结果保留根号)
解方程:  .
.