已知：如图①，在平行四边形ABCD中，AB=12，BC=6，AD⊥BD．以AD为斜边在平行四边形ABCD的内部作Rt△AED，∠EAD=30°，∠AED=90°．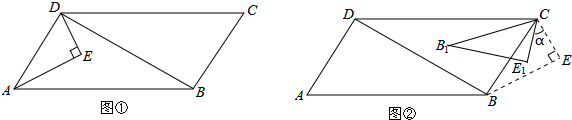
（1）求△AED的周长；
（2）若△AED以每秒2个单位长度的速度沿DC向右平行移动，得到△A0E0D0，当A0D0与BC重合时停止移动，设运动时间为t秒，△A0E0D0与△BDC重叠的面积为S，请直接写出S与t之间的函数关系式，并写出t的取值范围；
（3）如图②，在（2）中，当△AED停止移动后得到△BEC，将△BEC绕点C按顺时针方向旋转α（0°＜α＜180°），在旋转过程中，B的对应点为B1，E的对应点为E1，设直线B1E1与直线BE交于点P、与直线CB交于点Q．是否存在这样的α，使△BPQ为等腰三角形？若存在，求出α的度数；若不存在，请说明理由．
一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为
，两车之间的距离为
，图中的折线表示
与
之间的函数关系．
根据图象进行以下探究
（1）请解释图中点
的实际意义；
（2）求慢车和快车的速度；
（3）求线段BC所表示的与之间的函数关系式，并写出自变量的取值范围；
在矩形纸片ABCD中，AB=6，BC=8，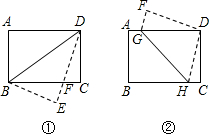
（1）将矩形纸片沿BD折叠，使点A落在点E处（如图①），设DE和BC相交于点F，试说明△BDF为等腰三角形，并求BF的长；
（2）将矩形纸片折叠，使B与D重合（如图②）求折痕GH的长。
如图，直线
：y=3x+1与直线
：y=mx+n相交于点P（1，b）．
（1）求b的值；
（2）不解关于x，y的方程组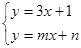
请你直接写出它的解；
（3）直线
：y=nx+m是否也经过点P？请说明理由．
(8分)如图，一直线BC与已知直线AB：
关于y轴对称。
（1）求直线BC的解析式；
（2）说明两直线与x轴围成的三角形是等腰三角形。
如图，O为矩形ABCD的对角线的交点，DE∥AC，CE∥BD，
（1）试判断四边形OCED的形状，并说明理由；
（2）若AB=3，BC=4，求四边形OCED的面积。