如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.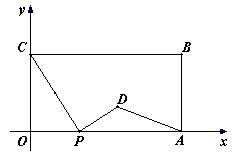
(1)请用含t的代数式表示出点D的坐标;
(2)求t为何值时,△DPA的面积最大,最大为多少?
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
(4)请直接写出随着点P的运动,点D运动路线的长.
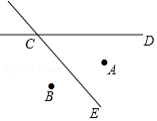
两个城镇 , 与一条公路 ,一条河流 的位置如图所示,某人要修建一避暑山庄,要求该山庄到 , 的距离必须相等,到 和 的距离也必须相等,且在 的内部,请画出该山庄的位置 .(不要求写作法,保留作图痕迹.
如图,点 , 分别在菱形 的边 , 上,且 .
求证: .

如图,13个边长为1的小正方形,排列形式如图,把它们分割,使分割后能拼成一个大正方形.请在如图所示的网格中(网格的边长为 中,用直尺作出这个大正方形.

如图,抛物线 与 轴交于 , 两点,与直线 交于 , 两点,直线 与抛物线的对称轴交于点 .
(1)求抛物线的解析式;
(2)若点 在直线 上方的抛物线上运动.
①点 在什么位置时, 的面积最大,求出此时点 的坐标;
②当点 与点 重合时,连接 ,将 补成矩形,使 上的两个顶点成为矩形一边的两个顶点,第三个顶点落在矩形这一边的对边上,求出矩形未知顶点的坐标.

在 中, , 是 上一点,连接 ,作 ,使 ,且 ,过点 作 交 于 ,连接 .
(1)如图1.
①连接 ,求证:
②若 是线段 的中点,且 , ,求 的长;
(2)如图2,若点 在线段 的延长线上,且四边形 是矩形,当 , 时,求 的长(用含 , 的代数式表示).
