在平面直角坐标系中,抛物线C :y=
:y= x
x +4x+4
+4x+4 (0<
(0< <2),
<2),

(1)当C 与x轴有唯一交点时,求C
与x轴有唯一交点时,求C 的解析式;
的解析式;
(2)若 =1,将抛物线C
=1,将抛物线C 先向右平移2个单位,再向下平移1个单位得抛物线C
先向右平移2个单位,再向下平移1个单位得抛物线C ,抛物线C
,抛物线C 与x轴相交于M、N两点(M点在N点的左边),直线y=kx(k>0)与抛物线C
与x轴相交于M、N两点(M点在N点的左边),直线y=kx(k>0)与抛物线C 相交于P、Q(P在第三象限)且△NOQ的面积是△MOP的面积的4倍,求k的值;
相交于P、Q(P在第三象限)且△NOQ的面积是△MOP的面积的4倍,求k的值;
(3)若A(1,y ),B(0,y
),B(0,y ),C(-1,y
),C(-1,y )三点均在C
)三点均在C 上,连BC,作AE∥BC交抛物线C
上,连BC,作AE∥BC交抛物线C 于E,求证:当
于E,求证:当 值变化时,E点在一条直线上.
值变化时,E点在一条直线上.
如图,反比例函数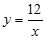 的图像与一次函数y=kx+4的图像相交于P、Q两点,并且P点的纵坐标是6.
的图像与一次函数y=kx+4的图像相交于P、Q两点,并且P点的纵坐标是6.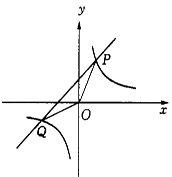
(1)求这个一次函数的解析式
(2)求△POQ的面积.
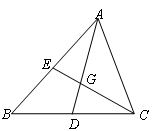
如图,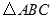 中,
中,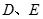 分别是边
分别是边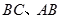 的中点,
的中点,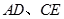 相交于
相交于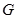 .
.
求证: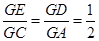 .
.
已知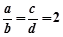 ,求
,求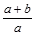 和
和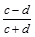 的值。
的值。
在△ABC中,AB=CB,∠ABC=90º,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30º,求∠ACF度数.
请完成下面的说明:(1)如图①所示,△ABC的外角平分线交于G,试说明∠BGC=90°- ∠A.
∠A.
说明:根据三角形内角和等于180°,可知∠ABC+∠ACB=180°-∠_____.
根据平角是180°,可知∠ABE+∠ACF=180°×2=360°,
所以∠EBC+∠FCB=360°-(∠ABC+∠ACB)=360°-(180°-∠_____)=180°+∠______.
根据角平分线的意义,可知∠2+∠3= (∠EBC+∠FCB)=
(∠EBC+∠FCB)= (180°+∠_____)=90°+
(180°+∠_____)=90°+ ∠_______.
∠_______.
所以∠BGC=180°-(∠2+∠3)=90°-∠____.
(2)如图②所示,若△ABC的内角平分线交于点I,试说明∠BIC=90°+ ∠A.
∠A.
(3)用(1),(2)的结论,你能说出∠BGC和∠BIC的关系吗?