(本小题满分12分)某车间要加工某种零件,现将 名技工平均分为甲、乙两组,分别标记为
名技工平均分为甲、乙两组,分别标记为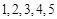 号,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
号,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
| |
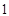 号技工 号技工 |
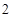 号技工 号技工 |
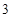 号技工 号技工 |
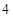 号技工 号技工 |
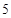 号技工 号技工 |
| 甲组 |
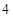 |
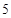 |
 |
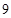 |
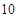 |
| 乙组 |
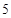 |
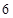 |
 |
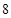 |
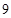 |
(Ⅰ)分别求出甲、乙两组技工在单位时间内完成合格零件的平均数及方差,并由此比较两组技工的技术水平;
(Ⅱ)质检部门从该车间甲、乙两组中各随机抽取 名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过
名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过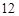 件,则称该车间“质量合格”,求该车间“质量合格”的概率.
件,则称该车间“质量合格”,求该车间“质量合格”的概率.
(本小题满分12分)学校文娱队的每位队员唱
歌、跳舞至少会一项,已知会唱歌的有2人,会跳舞的有5人,现从中任选2人.设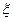 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且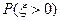 =.
=.
(Ⅰ)求文娱队的人数;
(Ⅱ)写出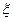 的概率分布列并计算
的概率分布列并计算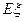 .
.
(本小题满分12分) 一几何体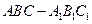 的三视图如图所示,
的三视图如图所示,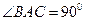 ,A1A=
,A1A=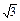 ,AB=
,AB=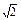 ,AC=2,A1C1=1,
,AC=2,A1C1=1,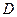 在线段
在线段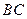 上且
上且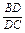 =
=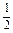 .
.
(I)证明:平面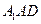 ⊥平面
⊥平面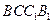 ;
;
(II)求二面角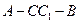 的余弦值.
的余弦值.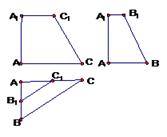
(本小题满分12分)数列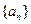 是首项
是首项 的等比数列,且
的等比数列,且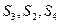 成等差数列.
成等差数列.
(I)求数列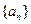 的通项公式;
的通项公式;
(II)设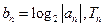 为数列
为数列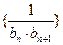 的前
的前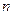 项和,求
项和,求 .
.
(本小题满分10分) 设命题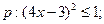 命题
命题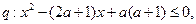 若
若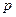 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数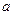 的取值范围.
的取值范围.
已知数列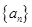 的前
的前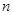 项和为
项和为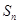 ,且
,且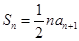 (
(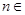 N*),其中
N*),其中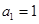 .
.
(Ⅰ)求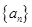 的通项公式;
的通项公式;
(Ⅱ) 设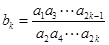 (
(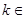 N*).
N*).
①证明: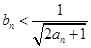 ;
;
② 求证: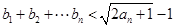 .
.