如图，△ABC中，∠ACB=90°，AC=6，BC=8．点P从A点出发沿A﹣C﹣B路径向终点运动，终点为B点；点Q从B点出发沿B﹣C﹣A路径向终点运动，终点为A点．点P和Q分别以1和3的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．问：点P运动多少时间时，△PEC与QFC全等？请说明理由．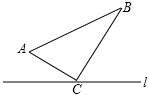
课桌的高度比标准高度高2毫米记作+2毫米，那么比标准高度低3毫米记作什么？
现有5张课桌，量得它们的尺寸比标准尺寸长1毫米，-1毫米，0毫米，+3毫米，-1．5毫米，若规定课桌的高度最高不能高于标准高度2毫米，最低不能低于标准高度2毫米，才算合格，问上述5张课桌有几张不合格？
下图中的两个圆分别表示正数集合和分数集合，请你在每个圆中及它们重叠的部分各填入3个数．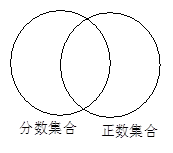
把下列各数填入相应的大括号内：-13．5，2，0，0．128，-2．236，3．14，+27，-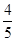
，-15%，-1
，
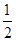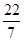，26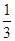
．
正数集合{…}，负数集合{…}，
整数集合{…}，分数集合{…}，
非负整数集合{…}．
你能估算一粒小米的重量吗？
①用小碗盛一碗米，放入较大的容器中，再放入100颗绿豆，搅拌均匀.
②从中取出一小部分，数一数其中绿豆多少颗，小米多少颗.
③算出绿豆所占的百分比P.
④若小米总颗数为x，则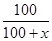
=P，可求出x=
.
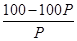⑤取一合适筛子将小米全部筛出.
⑥称出小米总重量G.
⑦每粒小米重量约为
.
（1）试用所学知识解释这种方法，估计一粒小米重量的合理性.
（2）说说这一实验的注意事项.
（3）将以上操作做怎样调整，便可不用作第⑤步了.
一盘残棋，小明通过数右上角一部分白棋子占60%，他又数了白棋子一共是87个，从而算出黑棋子大约有58个.
（1）你同意这种估算方法吗？说明理由.
（2）你有更合理的估算方法吗？试设计一种方案.