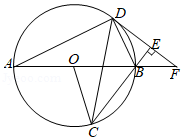
如图1,在△ABC,∠A=45°,延长CB至D,使得BD=BC.
(1)若∠ACB=90°,求证:BD=AC;
(2)如图2,分别过点D和点C作AB所在直线的垂线,垂足分别为E、F,求证:DE=CF;
(3)如图3,若将(1)中“∠ACB=90°”改为“∠ACB=m°,并在AB延长线上取点G,使得∠1=∠A”.试探究线段AC、DG的数量与位置关系.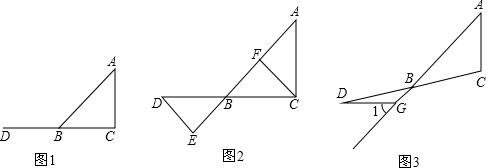
先化简,再求值: ,其中 .
已知抛物线 与 轴交于点 和 ,与 轴交于点 ,顶点为 ,点 在抛物线对称轴上且位于 轴下方,连 交抛物线于 ,连 、 .
(1)求抛物线的解析式;
(2)如图1,当 时,求 点的横坐标;
(3)如图2,过点 作 轴的平行线 ,过 作 于 ,若 ,求 点的坐标.

已知等边三角形 ,过 点作 的垂线 ,点 为 上一动点(不与点 重合),连接 ,把线段 绕点 逆时针方向旋转 得到 ,连 .
(1)如图1,直接写出线段 与 的数量关系;
(2)如图2,当点 、 在 同侧且 时,求证:直线 垂直平分线段 ;
(3)如图3,若等边三角形 的边长为4,点 、 分别位于直线 异侧,且 的面积等于 ,求线段 的长度.
某商贸公司购进某种商品的成本为20元 ,经过市场调研发现,这种商品在未来40天的销售单价 (元 与时间 (天 之间的函数关系式为: ,且日销量 与时间 (天 之间的变化规律符合一次函数关系,如下表:
|
时间 (天 |
1 |
3 |
6 |
10 |
|
|
日销量 |
142 |
138 |
132 |
124 |
|
(1)填空: 与 的函数关系为 ;
(2)哪一天的销售利润最大?最大日销售利润是多少?
(3)在实际销售的前20天中,公司决定每销售 商品就捐赠 元利润 给当地福利院,后发现:在前20天中,每天扣除捐赠后的日销售利润随时间 的增大而增大,求 的取值范围.
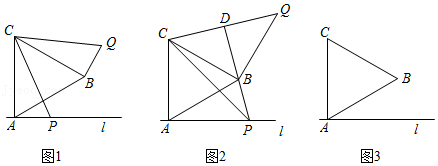
如图,已知 是 的直径, 为 上一点, 的角平分线交 于点 , 在直线 上,且 ,垂足为 ,连接 、 .
(1)求证: 是 的切线;
(2)若 , 的半径为3,求 的长.