如图a所示的平面坐标系xOy,在整个区域内充满了匀强磁场,磁场方向垂直坐标平面,磁感应强度B随时间变化的关系如图b所示。开始时刻,磁场方向垂直纸面向内(如图),t=0时刻有一带正电的粒子(不计重力)从坐标原点O沿x轴正向进入磁场,初速度为v0=2×103m/s。已知带电粒子的比荷为 ,其它有关数据见图中标示。试求:
,其它有关数据见图中标示。试求: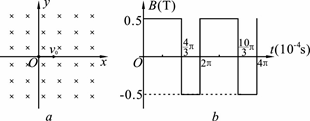
(1)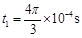 时粒子所处位置的坐标(x1,y1);
时粒子所处位置的坐标(x1,y1);
(2)带电粒子进入磁场运动后第一次到达y轴时离出发点的距离h;
(3)带电粒子是否还可以返回原点?如果可以,求返回原点经历的时间t′。
(9分)质量为m=35kg的小孩坐在M=15kg的雪橇上,大人用与水平方向成θ=37°斜向上的拉力拉雪橇,力的大小为F=100N,雪橇与地面间的动摩擦因数为μ=0.15,(sin37°=0.6,cos37°=0.8,g=10m/s2)求:
(1)雪橇对地面的压力大小FN;
(2)雪橇运动的加速度大小a;
(3)大人持续向前拉雪橇x=14m时的速度v的大小。
(9分)一物体受到竖直向上拉力F的作用由静止开始向上运动,如图所示,当拉力F=42N时,物体向上的加速度a=4.0m/s2,不计空气阻力,g取10m/s2。求:
(1)前2s内的位移x的大小; (2)第2s末的速度v的大小; (3)物体的质量m。
用一沿斜面向上的恒力F将静止在斜面底端的物体向上推,推到斜面中点时,撤去F,物体正好运动到斜面顶端并开始返回。在此情况下,物体从底端到顶端所需时间为t,从顶端滑到底端所需时间也为t。若物体回到底端时速度为10m/s,试问:
(1)推力F与物体所受斜面摩擦力Ff之比为多少?
(2)斜面顶端和底端的高度差h为多少?
如图所示,半径R=0.5m的光滑圆环上套有一质量为m=0.1kg的小环,当圆环绕着过环心的竖直轴匀速旋转时,若环每秒钟恰好转过2圈,求小环偏离圆环最低点的高度h。(取g≈π2)
如图所示,某人用轻绳牵住一只质量 =0.6kg的氢气球,因受水平风力的作用,系氢气球的轻绳与水平方向成
=0.6kg的氢气球,因受水平风力的作用,系氢气球的轻绳与水平方向成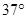 角。已知空气对气球的浮力为15N,人的质量
角。已知空气对气球的浮力为15N,人的质量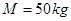 ,且人受的浮力忽略。(sin370=0.6,cos370=0.8,g=10m/s2)求:
,且人受的浮力忽略。(sin370=0.6,cos370=0.8,g=10m/s2)求: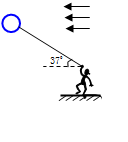
(1)在答卷上画出气球的受力分析图,并求出水平风力的大小
(2)通过计算说明,若水平风力增强,人对地面的压力如何变化?